In my last
post, I provided several arguments why the inference of U is logically
invalid. As a quick rehash, many (perhaps
most) of the big problems in foundational physics arise from an assumption (“U”)
that the quantum mechanical wave function always evolves linearly or unitarily,
so that when a small object in quantum superposition interacts with a large system,
the large system “inherits” the superposition.
Because U asserts that this is always true, no matter how big the
system, then cats (like Schrodinger’s Cat) and people (like Wigner’s Friend)
can exist in weird macroscopic superposition states. This is a problem because, well, we never
observe cats or anything else in superposition in our ordinary lives! There are lots more problems and weird
implications that follow from U, so it’s amazing just how few people have (at
least in the academic literature) questioned U.
Today’s post is my attempt to actually disprove U. I use a variety of novel logical arguments to
show that U is actually false -- or, at least, empirically unverifiable, which would
place it outside the realm of science. Together,
these posts will be put together and submitted as a journal article even if that
minimal effort is
unrewarded.
III. A NEW
LOGICAL ARGUMENT AGAINST U
In Section II, I attempted to show that U is not scientifically
justified as a valid inference because relevant empirical evidence supports
only ¬U. In this section, I will present
a new logical argument attempting to show an example in which U cannot be
experimentally verified even in principle.
In other words, not only does U lack experimental verification, I will
argue that U cannot be experimentally verified. I will first discuss the nature of a quantum
superposition from a logical standpoint, then address the extent to which
quantum superpositions must be relative.
Finally, I will present three variations on the argument.
A brief caveat: this argument is more likely to benefit
the skeptics of U than of its devoted adherents. Consider this statement: “A scalable
fault-tolerant quantum computer can be built.”
Let’s assume for the moment that it is in fact false, and could
logically be shown to be false because of some inconsistency with other facts
about the universe, but happens to be empirically unfalsifiable. Those who are already convinced that the
statement is true will be unlikely to be persuaded by a priori logical
argumentation. If they are in the field
of quantum computing, they may be responsible for directing private and public
funding toward achievement of a fundamentally unfulfillable goal. Waiting either for success or empirical
falsification, they continue to throw good money after bad, depriving more
viable scientific goals of funding.
Such is the case with the assumption of U. If U is in fact false, but turns out to be
empirically unfalsifiable, then any logical argument against U will probably
not be compelling to anyone who is already convinced of U. Instead, the following arguments are probably
most accessible and relevant to those scientists who are already skeptical of
U. Throughout the following analyses, I
will simply assume U true and show how that assumption leads to logical problems.
A. What is
a Quantum Superposition?
Let’s return to the double-slit interference experiment
in which a particle passes through a plate having slits A and B and assume that
the experiment is set up so that the wave state emerging from the plate is (unnormalized)
state |A> + |B>. What does that
mean? |A> represents the state the
particle would be in if it were localized in slit A, while |B> represents
the state the particle would be in if it were localized in slit B. If the particle had been in state |A>, for
example, then a future detection of that particle would be consistent with its
having been localized in slit A.
However, superposition state |A> + |B> is not the
same as state |A>. In other words,
state |A> + |B> is not the state of the particle localized in slit A, nor
is it the state of the particle localized in slit B. However, it is also not the state of the
particle not localized in slit A (because if it were not in A, it would
be in B), nor is it the state of the particle not localized in slit
B. Therefore, for a particle in state
|A> + |B>, none of the following statements is true:
·
The particle is in slit A;
·
The particle is not in slit A;
·
The particle is in slit B;
·
The particle is not in slit B.
While these statements may seem contradictory, the
problem is in assuming that there is some fact about the particle’s location in
slit A or B. Imagine two unrelated
descriptions, like redness (versus blueness) and hardness (versus softness). “Red is hard” and “red is soft” might seem
like mutually incompatible statements, one of which must be true and the other
false, but of course they are nonsensical because there just is no fact about
the hardness of red, or the redness of soft, etc. Analogously, for a particle in state |A> +
|B>, there just is no fact about its being localized in slit A or B. The problem is in assuming that “The particle
is in slit A” is a factual statement – that there exists a fact about whether
or not the particle is in slit A.
Unfortunately, the assertion that there exists such a fact is itself
incompatible with the particle being in state |A> + |B>.
Note also that state |A> + |B> is not a
representation of lack of knowledge; it does not mean that the state is
actually |A> or |B> but we don’t know which, nor does it have anything to
do with later discovering, via measurement, which of state |A> or |B> was
correct. If an object is in fact in a
superposition state now, a future measurement does not retroactively change that
fact. (See, e.g., Knight (2020).)
If an object is in state |A> + |B>, then there just
is no fact about its being in state |A> or |B> – not that we don’t know,
not that it is unknowable, but that such a fact simply does not exist in the
universe. This counterintuitive notion
inevitably leads many to confusion.
After all, if a cat could exist in state |alive> + |dead>, and if
that state is properly interpreted as there being no fact about its being alive
or dead, what does that say about the cat?
Wouldn’t the cat disagree? And what
quantum state would the cat assign to you?
Of course, if SC turns out to be
impossible to create, even in principle, then these worries disappear.
B. Relativity
of Quantum Superpositions
In the above example, |A> represented the state the
particle would be in if it were localized in slit A. To be more technical, |A> is an eigenstate
of the position operator corresponding to a semiclassical localization at
position A. But where exactly is “position
A”? If there is one thing that Galileo
and Einstein collectively taught us, it’s that positions (among other
measurables) are relative. That
recognitional already instructs us that state |A> + |B> is meaningless
without considering that the locations of positions A and B are relative to
other objects in the universe. In other
words, quantum superpositions are inherently relative. There are two types of relativity of quantum
superpositions I’ll discuss:
·
Weak Relativity of quantum superpositions:
Measurement outcomes (eigenstates of an observable) are relative to other
measurement outcomes.
·
Strong Relativity of quantum superpositions:
Essentially an extension of Galilean and Einsteinian Equivalence Principles, Strong
Relativity requires that if a first system (such as a molecule) is in a
superposition from the perspective of a second system (such as a laboratory),
then the second system is in a corresponding superposition from the perspective
of the first system. For instance, if a microscopic
object is in a superposition of ten distinct momentum eigenstates relative to a
measuring device, then the measuring device is conversely in a superposition of
ten distinct momentum eigenstates relative to the microscopic object.
While the notion of “quantum reference frames” is not new
(Aharanov and Kaufherr (1984) and Rovelli (1996)), the above notion of Strong
Relativity has only recently been discussed in the academic literature (Giacomini
et al. (2019), Loveridge et al. (2017), and Zych et al.
(2018)). If it is true, then it’s
relatively easy to show, as I did in this paper, that SC is a myth
and that macroscopic quantum superpositions cannot be demonstrated in
principle. In a sense, the truth of
Strong Relativity excludes the possibility of SC nearly as tautology, since if
a lab from whose perspective a cat is in state |alive> + |dead> can
equivalently be viewed from the perspective of the cat, then which cat? And what quantum state would describe the lab
from the cat’s perspective? From the
perspective of the live cat, perhaps the cat would view the lab in the
superposition state:
|lab that would measure me (the cat) as live> + |lab
that would measure me (the cat) as dead>
And if we think that cat states |alive> and |dead>
are interestingly distinct, can you imagine how incredibly and weirdly distinct
those eigenstates would seem from the perspective of the live cat? Rewriting the above state with a little more
description, the lab would appear from the live cat’s perspective as state:
|lab that would measure me (the cat) as live, which isn’t
surprising, because I am alive> +
|lab that is so distorted, whose measuring devices are so
defective, whose scientists are so incompetent, that it would measure me (the
cat) as dead>
The second eigenstate is actually far worse than
described. Every single measurement made
by that lab would have to correspond, from its perspective, to a dead cat; the
scientists in it, when looking at the cat, when receiving and processing
trillions of photons bouncing off the cat, would have to see a dead cat! And it’s worse than that. Even when the scientists leave the lab, the
universe requires that the story stays consistent; no future fact about the
lab, its measuring devices, or its scientists – or anything they interact with
in the future – can conflict with their observation of a dead cat, even though
that second eigenstate is from the perspective of a live cat!
I derived the notion of Strong Relativity independently and
therefore regard it as nearly obviously true.
Nevertheless, because it is by no means universally accepted (or even
known) by physicists or philosophers, I won’t depend on it in this paper. Instead, I’ll use Weak Relativity, which is
obviously and necessarily true. For
instance, a particle is only vaguely specified by state |A> + |B>. For a scientist S in a laboratory L who plans
to use measuring device M to detect the particle whose state |A> + |B>
references positions A and B, we should be asking whether positions A and B are
localized relative to the measuring device M, the lab L, the scientist S,
etc. In other words, is the particle in
state |A>M + |B>M, |A>L + |B>L,
or |A>S + |B>S?
Why does this matter?
Surely position A is the same position relative to the measuring
device, lab, and scientist. And for
essentially all practical purposes, that’s true, which is probably why the
following analysis is absent from the academic literature. After all, how could the measuring device,
scientist, etc., disagree about the location of position A?
As discussed in Section II, quantum uncertainty disperses
a wave packet, so over time a well-localized object tends to get “fuzzy” or
less well localized. Why don’t we notice
this effect in our ordinary world? What
keeps the scientist from becoming delocalized relative to the lab and measuring
device? First, the effect is inversely
related to mass. We barely notice the
effect on individual molecules, so we certainly won’t notice it with anything
we encounter on a daily basis. Second,
events, such as impacts with photons, air molecules, etc., are constantly
correlating objects to each other and thus decohering relative superpositions. For example, the air molecules bouncing
between the scientist and measuring device are constantly “measuring” them
relative to each other, preventing their wave packets from dispersing relative
to each other.
So while the scientist might in principle be delocalized
from the measuring device by some miniscule amount, that amount is much, much,
much smaller than could ever be measured, and is therefore irrelevant to
whether position A is located relative to the scientist S, the measuring device
M, or the lab L. Therefore, it’s usually
fine to write state |A> + |B> instead of |A>M + |B>M,
etc., because |A>M + |B>M ≈ |A>L +
|B>L ≈ |A>S + |B>S.
However, if U is true, then producing SC or WF (and
correspondingly enormous relative delocalizations) are actual physical
possibilities, if perhaps very difficult or impossible to achieve in
practice. If we’re going to talk about
cat state |alive> + |dead>, or a superposition of a massive object in
position eigenstates so separated that they would produce distinct
gravitational fields (Penrose (1996)), or macroscopic quantum superpositions in
general, then we can no longer be sloppy about how (i.e., in relation to what)
we specify a superposition of eigenstates.
That said, I’ll now argue how keeping track of these relations between
systems implies that there are at least some macroscopic quantum superpositions
(such as SC) that cannot be measured or empirically verified, even in
principle.
C. The
Argument in Words
A scientist S (initially in state |S>) wants to
measure the position of a tiny object O.
The object O is in a superposition of position eigenstates
corresponding to locations A and B, separated by some distance d,
relative to the scientist S. Neglecting
normalization constants, |O> = |A>S + |B>S. To measure it, he uses a measuring device M (initially
in state |M>) configured so that a measurement of the position of object O
will correlate device M and object O so that device M will then evolve over
(some brief but certainly nonzero) time to a corresponding macroscopic pointer
state, denoted |MA> or |MB>. Device M in state |MA>, for
example, indicates “A” such as with an arrow-shaped indicator pointing at the
letter “A.” In other words, device M is
designed/configured so that if M measures object O at location A, then M will,
through a causal chain that amplifies the measurement, evolve to some state
that is very obviously different to the scientist S than the state to which it
would evolve had it measured object O at location B. The problem, reflecting Weak Relativity, is
that device M measures the location of object O relative to it. Relative to device M, the object O is in
state |A>M + |B>M, which means that a correlating
event between O and M will cause M to evolve into a state in which macroscopically
indicating “A” correlates to its measurement of the object at position A
relative to M, and vice versa for position B.
Of course, this doesn’t typically matter in the real
world. The scientist S is already well
localized relative to device M; there is essentially no quantum fuzziness
between them. Because |A>M
+ |B>M ≈ |A>S + |B>S, measurement of
the object O at A relative to M is effectively the same as its measurement
relative to S, so the device’s macroscopic pointer state will properly
correlate to the object’s location at position A or B relative to S, which was
exactly what the scientist wanted to measure.
However, under what circumstances would it matter whether |A>M
+ |B>M ≠ |A>S + |B>S, and how could
this situation come to pass?
Let’s say that the experiment is set up at time t0;
then at time t1 the device M “measures” the object O via some
initial correlation event, after which M then evolves in some nonzero time Δt
to a correlated macroscopic pointer state; and then at t2 the
scientist S reads the device’s pointer.
Under these normal circumstances, at time t0,
object O is in a superposition relative to both M and S. (Said another way, relative to M and S, there
is no fact at t0 about the location of O at A or B.) Its being in a superposition is what makes
possible an interference experiment on O to demonstrate its superposition
state. Skipping ahead to time t2,
the scientist S is correlated to M and O – i.e., the object’s position at B,
for example, is correlated with the device’s pointer indicating “B” and the
scientist’s observation of the device indicating “B.” At time t2, object O is no longer
in a superposition relative to either M or S.
(Said another way, relative to M and S, there is a fact at t2
about the location of O at position A or B.)
Consequently, at t2 it is not possible, even in principle,
for the scientist S to do an interference experiment on object O or device M to
demonstrate a superposition, because they aren’t. It is not a question of difficulty; I am
simply noting the (hopefully uncontroversial) claim that by time t2,
the position of object O is already correlated to that of the scientist S, so
he now cannot physically demonstrate, via an interference experiment, that
there is no fact about O’s location at A or B relative to him.
Let me summarize.
At t0, object O is in a superposition relative to S, so
scientist S could in principle demonstrate that with a properly designed
interference experiment. Device M,
however, is well localized relative to S, so scientist S would be incapable at t0
of showing M to be in a superposition.
At t2, neither O nor M is in a superposition relative to S,
so S obviously cannot perform an interference experiment to prove otherwise. The only question remaining is: what is the
state of affairs at time t1 (or t1+Δt)? The standard narrative in quantum mechanics,
which follows directly from the assumption of U, is the following von Neumann
chain:
Equation 1:
t0: |O>
|M> |S>
=
(|A> + |B>) |M> |S>
t1 (or t1+Δt): (|A> |MA> + |B> |MB>)
|S>
t2: |A>
|MA> |SA> + |B> |MB> |SB>
According to Eq. 1, at time t1 object O and
device M are correlated to each other but scientist S is uncorrelated to O and
M. Said another way, O and M are well
localized relative to each other (i.e., there is a fact about O’s location
relative to M) but S is not well localized to O or M (i.e., there is not
a fact about the location of O or M relative to S). If that is true, then scientist S would be
able, at least in principle, in an appropriate interference experiment, to
demonstrate that object O and device M are in a superposition relative to
him. No one claims that such an
experiment would be easy, but as long as there is some nonzero time period (in
this case, t2 - t1) in which such an experiment could be
done, then maybe it’s just a question of technology. The problem, as I will explain below, is that
there is no such time period. The
appearance of a nonzero time period (t2 – t1) in Eq. 1 is
an illusion caused by failure to keep track of what the letters “A” and “B”
actually refer to in each of the terms.
Let’s assume Eq. 1 is correct: that at time t1,
the location of O is correlated to M but is not correlated to S. That means that the location at which M
measured O, which is what determines the macroscopic pointer state to which M
will evolve, is not correlated to the location of O relative to S. Consequently, the macroscopic pointer state
to which M will evolve will correlate to the location of O relative to M at t1,
but because that location of O (relative to M) is not correlated to its
location relative to S, the macroscopic pointer state of M will itself be
uncorrelated to O’s location relative to S.
Then, at t2, S’s observation of M’s pointer will therefore be
uncorrelated to O’s location relative to him.
Let me reiterate.
Object O is in a superposition of position eigenstates |A>S
and |B>S relative to scientist S.
He asks a simple question: “Will I find it in position A or B?” To answer the question, he uses a measuring
device M that is designed to measure the object’s position and indicate either
output “A” or “B.” But if Eq. 1 is
correct, then when he looks at the device’s output, a reading of “A” does not
tell him where the object was measured relative to him, which is what he
was trying to determine! Rather, the
device’s output tells him where the object was measured relative to the device,
to which, at time t1, he was uncorrelated.
If Eq. 1 is correct at t1 that M is in a
superposition relative to S (by virtue of its entanglement with object O), then
the device’s measurement and subsequent evolution are uncorrelated to the
location of object O relative to scientist S.
In other words, if Eq. 1 is correct, then as far as scientist S is
concerned, measuring device M didn’t measure anything at all. Instead, the macroscopic output of the device
M would only correlate to the object’s location relative to S if M was well
correlated to S at time t1, in which case Eq. 1 is wrong.
I should stress that the current narrative in physics is
not just that Eq. 1 is possible, but that a comparable von Neumann chain occurs
in every quantum mechanical measurement, big or small. At t1, device M, but not scientist
S, is correlated to the position of object O.
But what I’ve just shown is that if that’s true, then the position of O
to which M is correlated is a different position of O than the scientist
S intended to measure, such that the device’s output will necessarily be
uncorrelated – and thus irrelevant – to the scientist’s inquiry. If Eq. 1 is correct – if macroscopic device
M, which is correlated to object O, can be in a superposition relative to scientist
S – then measuring devices aren’t necessarily measuring devices and the very
foundations of science are threatened.
Conundrum as this may be, it’s not even the whole problem
with Eq. 1. We have to ask how it
could be that the measuring device failed.
Remember that what the scientist wants to measure is the object in state
|A>S or |B>S, but the device M is only capable of
measuring the object in state |A>M or |B>M. When he starts the experiment at t0,
he and device M are already well correlated, the presumption being that a
measurement by the device of |A>M, when observed by the scientist,
will correlate to |A>S.
But if Eq. 1 is correct, then the correlation event at t1 is
one that guarantees that this can’t happen, which means that at t1,
|A>M ≠ |A>S.
So even though |A>M ≈ |A>S at t0,
Eq. 1 implies that |A>M ≠ |A>S at t1
(and by a significant distance). That
is, the quantum fuzziness between device M and scientist S (both macroscopic
systems) would have to grow from essentially zero to a dimension comparable to
the distance d separating locations A and B. The analysis in Section II, particularly regarding
relative coherence lengths and wave packet dispersion, shows that such a growth
over any time period, and certainly the short period from t0 to t1,
is impossible in principle.
Let me paraphrase.
At t1, device M has measured object O relative to it, so
there is a fact about O’s location relative to M. But if we stipulate as in Eq. 1 that there is
not a fact about O’s location relative to S (by claiming that it’s still
in a superposition relative to S), then what M has measured as position A
(|A>M) might very well correspond to what S would measure as
position B (|B>S) – or more generally, M’s indicator pointer will
not correlate to O’s location relative to S.
That just means that, at t1, M did not measure the location
of O relative to S. The only way this
could have happened is if |A>M and |A>S, which were
well correlated at time t0, had already become adequately uncorrelated
via quantum dispersion by time t1.
This is physically impossible.
Therefore Eq. 1 is incorrect: at no point can scientist S measure device
M in a superposition.
D. The
Argument in Drawings
In this section, I’ll provide a comparable logical
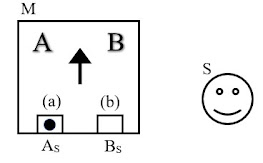
argument with reference to drawings. In Fig.
1a, object O is shown at time t0 in a superposition of position
eigenstates corresponding to locations at AS and BS
relative to scientist S, where the object O is shown crosshatched to represent
its superposition, relative to S, over two locations. Measuring device M has slots (a) and (b) and is
configured so that detection of object O in slot (a) will, due to a
semi-deterministic causal amplification chain, cause device M to evolve over
nonzero time Δt to a macroscopic pointer state in which a large arrow indicator
points to the letter “A,” and vice versa for detection of object O in slot
(b). Because the device’s detection of
object O in slot (a) actually corresponds to measurement of the object O at
location AM relative to M (and vice versa for slot (b)), the device
M is placed at time t0 so that AM ≈ AS and BM
≈ BS for the obvious reason that the scientist S intends to measure
the object’s location relative to him and therefore wants the device’s
indicator to correlate to that measurement.
Finally, the experiment is designed so that the initial correlation
event between object O and device M occurs at time t1, device M
evolves to its macroscopic pointer state by time t1+Δt, and
scientist S reads the device’s pointer at t2.

Fig. 1a
Figs. 1b and 1c show how the scientist might expect (and
would certainly want) the system to evolve.
In Fig. 1b, the locations of O relative to M and S are still well
correlated (i.e., AM ≈ AS and BM ≈ BS),
so the device’s detection of object O in slot (a) correlates to the object’s
location at AS. Then, in Fig. 1c, device M has evolved so
that the indicator now points to letter “A,” correlated to the device’s
detection of object O in slot (a). Then,
when scientist S looks at the indicator at time t2, he will observe
the indicator pointing at “A” if the object O was localized at AS
and “B” if it was localized at BS, which was exactly his intention
in using device M to measure the object’s position.
Fig. 1b Fig.
1c
Notice, however, that at time t1 the object O
is not in a superposition relative to S, nor is device M (which is correlated
to object O). At t1, object O
is indeed localized relative to device M, and since AM ≈ AS
and BM ≈ BS, it is localized relative to scientist S. We don’t know, of course, whether object O
was detected in slot (a) or (b), and Fig. 1b only shows the first possibility,
but it is in slot (a) or (b) (with probabilities that we can calculate
using the Born rule), with slot (a) correlated to AS (which is
localized relative to S) and slot (b) correlated to BS (which is
also localized relative to S). If that
weren’t the case, then object O’s position would still be uncorrelated to
device M, which negates the correlation event at t1. In other words, at time t1 in Fig.
1b, object O is localized at AS or BS – i.e., there is a
fact about its location relative to S – whether or not S knows this. Because object O is localized relative to S
at t1, S cannot do an interference experiment to show O in superposition,
nor can S show device M, which is correlated to O, in superposition.
Now, suppose we demand, consistent with Eq. 1, that at
time t1, scientist S can, in principle, with an appropriately
designed interference experiment, demonstrate that object O and device M are in
a superposition (relative to S). That
requirement implies that the object’s location, as measured by M via the
correlation event at t1, does not correlate to the object’s
location relative to S. The device’s
detection at t1 of the object O in, for example, slot (a), which
corresponds to its measurement of the object at AM, cannot correlate
to the location of the object at AS – otherwise S would be incapable
of demonstrating O (or M, to which O is correlated) in superposition. Thus, to ensure that object O remains
unlocalized relative to S when the correlation event at t1 localizes
object O relative to M, that location which M measures as AM by
detection of object O in slot (a) cannot correlate to location AS.
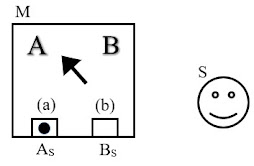
Fig. 2a
This situation is shown in Fig. 2a in which both object O
and device M are shown in a superposition of position eigenstates relative to
S. The object’s crosshatching, as in
Fig. 1a, represents its superposition, relative to S, over locations AS
and BS. Analogously (but
without crosshatching), device M localized at MA is shown
superimposed on device M localized at MB. Importantly, MA is the position of
device M that would measure the position of object O at AM (by
detecting it in slot (a)) as AS, while MB is the position
of device M that would measure the position of object O at AM (by
detecting it in slot (a)) as BS.
Because O remains uncorrelated to S at t1 (as demanded by Eq.
1), the measuring device M that detects O in slot (a) must also be uncorrelated
to S at t1. Again, the same
is true for device M that detects O in slot (b), which is not shown in Fig.
2a. What is demonstrated in Fig. 2a is
that the correlation event at t1 between device M and object O that
localizes O relative to M requires that M is not correlated to S, thus allowing
S to demonstrate M in a superposition, as required by Eq. 1. Then, in Fig. 2b, at time t1+Δt,
device M has evolved so that the indicator now points to letter “A,” correlated
to the device’s detection of object O in slot (a).

Fig. 2b
However, now we have a problem. In Fig. 2b, the pointer indicating “A,” which
is correlated to the device’s localization of object O at AM, is not
correlated to the object’s localization at AS. When the scientist S reads the device’s
indicator at time t2, it is not that the output is guaranteed to be
wrong, but rather that the output is guaranteed to be uncorrelated to the
measurement he intended to make. Worse,
it’s not just that the output is unreliable – sometimes being right and
sometimes being wrong – it’s that the desired measurement simply did not
occur. The correlation event at time t1
did not correlate the scientist to the object’s location relative to him.
Therefore, to guarantee that object O (and device M, to
which it is correlated) is in superposition relative to scientist S at t1,
as required by Eq. 1, the location AM as measured by device M cannot
correlate to location AS relative to scientist S; thus there is no
fact at t1 about whether the measurement at AM (which
will ultimately cause device M to indicate “A”) will ultimately correlate to
either of locations AS or BS relative to S. (Similarly, there is no fact at t1
about whether location BM will correlate to either AS or
BS.) That is only possible if
that location which device M would measure at t1 as AM
could be measured by scientist S as either AS or BS, which
is only possible if AM ≠ AS.
To recap: At t0 the scientist S sets up the
experiment so that AM ≈ AS and BM ≈ BS,
which is what S requires so that measuring device M actually measures what it
is designed to measure. If Eq. 1 is
correct, it implies that at time t1, AM ≠ AS
and BM ≠ BS.
This has two consequences. First, we need to explain how (and whether)
device M could become adequately delocalized relative to scientist S so that AM
≠ AS and BM ≠ BS in the time period from t0
to t1. Remember, we are not
talking about relative motion or shifts – we are talking about AM
and AS becoming decorrelated from each other so as to be in a
location superposition relative to each other.
In other words, how do AM and AS, which were well
localized relative to each other at time t0, become so “fuzzy”
relative to each other via quantum wave packet dispersion that AM ≠
AS at time t1?
They don’t. As long as the
relative coherence length between two objects is small relative to the distance
d separating distinct location eigenstates, then the situation in which
AM ≠ AS cannot happen over any time period.
Second, the quantum amplification in a von Neumann chain
depends on the ability of measuring devices to measure what they are intended
to measure. A state |A>S +
|B>S can only be amplified through entanglement with intermediary
devices if those terms actually become correlated to states |A>S
and |B>S, respectively. But
if, as required by Eq. 1, there is some nonzero time period (t2 - t1)
in which scientist S could in principle measure M and O in a superposition, then
the device’s measurement of the object’s location relative to it cannot
correlate to the object’s location relative to S, in which case future states
of S cannot be correlated to either |A>S or |B>S. Eq. 1 is internally inconsistent and is
therefore false. There is no time period
in which scientist S can measure M and O in a superposition.
E. The
Argument in Equations
A quick warning: as discussed in Section II(b), the QM
mathematical formulism is the cause of the measurement problem and
inherently cannot be part of the solution.
The problem with Eq. 1, which follows directly from U and has been shown
to be problematic in the previous sections, will not be apparent by using the
traditional tools and equations available in QM. In the following analysis I will explain and
adopt a new nomenclature that I hope will be helpful in relaying the arguments
of the prior sections.
Another quick warning.
The assumption that SC and WF, for example, are experimentally possible
in principle depends on the ability of an external observer to subject them to
a “properly designed interference experiment,” which is one in which the chosen
measurement basis is adequate to reveal interference effects between the separate
terms of the superposition. No one
denies that the required measurement basis for revealing a cat in superposition
over |dead> and |alive> states would be ridiculously complicated and
extremely technologically challenging. However, there are some, such as Goldstein
(1987), who claim that every measurement is ultimately a position
measurement. If so, then no experiment
could ever demonstrate a complicated macroscopic quantum superposition like SC. Further, as I’ll discuss in more detail in
Section F, the measurement basis required to demonstrate SC is also one that
guarantees that SC does not exist, leading to a contradiction that, I will
argue, renders moot any seeming logical paradox.
Regarding nomenclature: by state |A>S, I
mean the state of an object O that is located at position A relative to the
scientist S, by which I mean a state in which there is a fact about its
location relative to S, whether or not S knows it. And what does that mean? It means that if O is in state |A>S
at time t0, then S will not, after t0, make any
measurements, have any experiences, etc., that are inconsistent with that fact
or even, more importantly, any of its consequences. And that certainly includes interference
experiments. Because |A>S
is a state of object O located at position A relative to scientist S, it
implies a state of the scientist S that is correlated to the location of O at position
A relative to him. The scientist S in
that state, which I’ll write |SOA>, may or may not ever measure
the location of object O, but if he does, he will with certainty find object O
at position A (or somewhere that is logically consistent with the object having
been located at position A when the object was in state |A>S). Said differently, |A>S is a
state of object O in which scientist S would be incapable of measuring O in orthogonal
state |B>S, state |A>S + |B>S, or any
future state logically inconsistent with |A>S.
For instance, imagine if whether it rains today hinges on
some quantum event that is heavily amplified, such as by chaotic interactions. (Indeed, Albrecht and Phillips (2014) brilliantly
argue that all probabilistic effects, certainly including weather, are
fundamentally quantum.) Specifically,
imagine that a tiny object, located in Asia and in spin superposition |up> +
|down>, was “measured” by the environment in the {|up>,|down>} basis
by an initial correlating interaction or event, followed by an amplification
whose definite mutually exclusive outcomes, correlated to the object’s
measurement as “up” or “down,” are that it either will or will not,
respectively, rain today in Europe. If
that object were in fact in state |up>, in which case it will rain today in
Europe, then no observer would make any measurements or have any observations
that are inconsistent with that fact. Of
course, the observer in Europe would not immediately observe that fact or its
consequences, but once the fact begins to manifest itself in the world, that
observer will eventually observe its effects – notably rain. That observer – the one correlated to
observing rain – now lives in a universe in which he will not and cannot make a
contradictory observation (i.e., one logically inconsistent with the fact of
|up> or its consequences).
Of course, a superposition is fundamentally
different. For an object in state |A>S
+ |B>S, there is no fact about the object’s location at position
A or B relative to scientist S. While
|A>S is a state in which O is in fact located at A relative to S,
which implies that S is in state |SOA> that is correlated to the
location of O at position A relative to him, it is a mistake to assume that |SOA>
exists without |A>S – i.e., it is a mistake to assume that they
are already correlated prior to a correlating or entangling event. After all, prior to a correlation event, the
state of S can mathematically be written in lots of different bases, most of
which would be useless or irrelevant.
Even though it may be correct that an object O is in state |A>S
+ |B>S, that same superposition can be written in different measurement
bases, and the state in which O will be found upon measurement will depend on
the relevant measurement basis. So just
as O can be written in state |A>S + |B>S (among
others) and S can be written in state |SOA> + |SOB>
(among others), neither |A>S nor |SOA> come into
being until, in this case, a position measurement correlates them. Before the correlation event, there is no
object O in state |A>S just as there is no scientist S in state
|SOA>, while after the correlation event there is.
Let me elaborate.
If object O is in state |A>S + |B>S, then it
is in fact not in either state |A>S or |B>S, which
also means that the scientist S is not in state |SOA> or |SOB>. Remember that the scientist in state |SOA>,
if he measures object O, will with certainty find it at position A. But if object O is in fact in state |A>S
+ |B>S, there is no such scientist. That the state of O can be written as |A>S
+ |B>S implies that the state of S can be written as |SOA>
+ |SOB>. Just as object O
is in neither state |A>S nor |B>S (or, stated
differently, there is no object O in state |A>S or |B>S)
and there is therefore no fact about its location at A or B relative to S, we
can also say that scientist S is in neither state |SOA> nor |SOB>
and there is no fact about whether he would with certainty find O at position A
or B. Until a measurement event occurs
between O and S that correlates their relative positions, there is no scientist
S that would with certainty find object O at A (or B), just as there is no
object in state |A>S or |B>S. It’s not an issue of knowing which
state the scientist is in, for if S were actually in |SOA> or |SOB>
but did not know which, then he was mistaken about being in state |SOA>
+ |SOB>. That is, before
the correlation event, there is no scientist in state |SOA> or |SOB>. Rather, what brings states |SOA>
and |SOB> (as well as |A>S and |B>S) into
existence
is the event that correlates the relative positions of S and O:
Equation 2:
t0: |O>
|S> = (|A>S + |B>S) |S> = (|A>S
+ |B>S) (|SOA> + |SOB>)
= |A>S
|SOA> + |B>S |SOA>
+ |A>S |SOB> + |B>S |SOB>
t2 (event correlating their positions): |A>S |SOA> + |B>S |SOB>
Note that at time t0, the scientist in state
|S> is still separable (i.e., unentangled) with |O> and can, in
principle, demonstrate O in a superposition relative to him. However, the correlation event at t2
entangles S with O so that no scientist (whether in state |SOA>
or |SOB>) can measure O in a superposition. Mathematically, the correlation event
eliminates incompatible terms, leaving only state |SOA>
correlated to |A>S and state |SOB> correlated to
|B>S. States |B>S
and |SOA>, for example, are only incompatible from the
perspective of position measurement. If
the correlation event is one that measures O in a different basis, then each of
|B>S and |SOA> can be written in that basis and the
correlation event caused by the measurement will not necessarily eliminate all
terms. This point further underscores that writing
the state of S as |SOA> + |SOB>, and its expansion
in Eq. 2, are purely mathematical constructs until the event at t2
that correlates the positions of O and S brings |SOA> and |SOB>
into existence and allows us to eliminate incompatible terms.
Let’s return to the original example in which scientist S
utilizes intermediary device M at time t1 to measure the position of
object O relative to him, which is initially in state |A>S +
|B>S. Of course, Weak
Relativity requires that device M is only capable of measuring positions
relative to it, but scientist S has set up the experiment so that at time t0,
|A>M ≈ |A>S and |B>M ≈ |B>S. In the following nomenclature, |MOA>,
for example, is a state of device M correlated to localization of object O at
position AM (relative to M).
M in state |MOA> can certainly try to measure O in a basis
other than position, but the existence of M in state |MOA>
implies that O has already been localized at AM so that the outcome
of a subsequent measurement will not be inconsistent with its initial
localization at AM. It is
important to note that |MOA> is not itself a macroscopic pointer
state; rather, assuming device M is designed correctly, |MOA> is a
state that cannot evolve to a macroscopic pointer state correlated to object O
located at BM. In other
words, a macroscopic pointer state of M indicating “A” will be correlated to |MOA>
and not |MOB>. Therefore,
I’ll write that pointer state, which evolves from state |MOA>
over nonzero time Δt, as |MAOA>. Using this nomenclature, we can expect,
according to the assumption of U, the following von Neumann-style measurement
process:
Equation 3:
t0: (|A>S
+ |B>S) |M> |S> ≈ (|A>M + |B>M)
|M> |S>
= (|A>M + |B>M)
(|MOA> + |MOB>) (|SOA> + |SOB>)
t1 (event correlating positions of O and M): (|A>M |MOA> +
|B>M |MOB>) (|SOA> + |SOB>)
t1+Δt: (|A>M
|MAOA> + |B>M
|MBOB>) (|SOA> + |SOB>)
t2: |A>S
|MAOA> |SAOA> + |B>S
|MBOB> |SBOB>
At t1, the event between O and M correlates
their positions, thus eliminating incompatible terms and ultimately entangling
O with M so that they are no longer separable.
At t1, there is no M that can show O in a superposition (of
position eigenstates relative to M).
Eq. 3 assumes that the event correlating the scientist to
the rest of the system does not occur until time t2. It assumes that at t1, |S> is
separable from (i.e., unentangled/uncorrelated with) states of device M and object
O and remains separable until an entangling event at time t2. If that’s true, then while |S> can be
written as |SOA> + |SOB> (as above), it can also be
written in lots of incompatible ways whose mathematical relevance depends on
the nature of the measurement event that correlates S to M and O. However, for |S> to be separable at t1,
there cannot have already been an event that correlates S to M and O. Is that true? I will argue below that because M and S are
already very well correlated in position (i.e., |A>M ≈ |A>S
and |B>M ≈ |B>S),
the event at t1 correlating the positions of O and M is one in which
M measures the position of O relative to S, which ultimately correlates the
positions of O and S, preventing S from being able to measure O or M in a
relative superposition.
Prior to the correlation event at t1, object O
can be written as |A>M + |B>M (i.e., the position
basis relative to M), |P1>M + |P2>M
+ |P3>M + ... (i.e., the momentum basis relative to
M), and various other ways depending on the measurement basis. It is the correlation event that determines
which basis and thus brings into existence one set of possibilities versus
another. So it is the correlation event
between M and O, which measures O in the position basis relative to M, that
brings into actual existence states |A>M and |B>M. That is to say, after t1, states
|A>M and |MOB> are no longer compatible because O
in fact was measured in the position basis by M and state |A>M is
what was measured by |MOA> (just as state |B>M is
what was measured by |MOB>).
Relative to M at t1, O is no longer in superposition; it is
in fact located at either AM or BM. One might object with the clarification that
“it is in fact located at either AM or BM relative to
M,” but that’s redundant as positions AM or BM
already reflect reference to device M.
The correlation event at t1, as a matter of fact, localizes
the object O at either AM or BM. The only question is what meaning these positions
have, if any, for scientist S.
In other words, in an important sense, the event at t1
does correlate the scientist to the object: she now lives in a universe
in which O is located at AM or one in which O is located at BM,
because that is exactly what it means for her to say that device M
measured the position of O at t1. Said another way, she in fact lives in a
universe in which device M has measured object O at AM or one in
which M has measured O at BM, even though she does not yet know
which, and whether or not |A>M and |B>M are
semiclassical position eigenstates from her perspective. This is necessarily true, for that is exactly
what it means to assert that a measurement event at t1 correlates M
and O.
This point is so important and fundamental that it is
worth repeating. The statement, “M
measured the position of O,” where O was initially in state |A>M
+ |B>M, means that either O was localized at AM or else
at BM; if it did not measure O at one of those locations, then “M
measured O” has no meaning. So when M
measures O at t1, object O is no longer in superposition |A>M
+ |B>M; scientist S now lives in a world in which device M has
measured the position of object O, and that position is either AM or
BM, not a superposition.
Proponents of U and/or MWI are certainly free to say that M measured O
at both AM and BM in different worlds. Perhaps the universe “fissions” so that one
device, in state |MOA>, is correlated to the object located at AM
while another, in state |MOB>, is correlated to the object
located at BM. In that case,
scientist S also fissions so that one scientist – let’s call her state |SOAm>
– is correlated to |A>M |MOA> and another, in state
|SOBm>, is correlated to |B>M |MOB>.
Thus the object O at time t1 is not in
superposition |A>M + |B>M from the scientist’s (or
anyone’s) perspective, but that does not tell us anything about whether the
object O is in a superposition relative to scientist S or whether a position
measurement by S on O would have some guaranteed (if unknown) outcome. Specifically, consider the scientist in state
|SOAm> who is correlated to the object in state |A>M. If, for example, |A>M = |A>S
+ |B>S (in other words, if the location of O at AM is
itself a superposition over locations AS and BS) then O
remains in a superposition relative to S.
Scientist S would remain uncorrelated to the object’s position until
after she measures it. The problem with
this scenario is twofold, as broached in previous sections. First, if |A>M is indeed
uncorrelated to |A>S, then the device’s macroscopic pointer
state, as observed by the scientist at t2, will necessarily be
uncorrelated to the measurement that the scientist intended to make –
specifically, the location of O at AS or BS. But even if one is willing to reject the
phrase “quantum measurement” as an oxymoron, the bigger problem is that there
is no physical means, even in principle, by which states |A>M and
|A>S, which were well correlated at t0, could become
adequately uncorrelated by some arbitrary time t1.
So, given that |A>M ≈ |A>S
and |B>M ≈ |B>S at t0 through to time t1,
then just as the object O is no longer in superposition |A>M +
|B>M at t1, it is also not in superposition |A>S
+ |B>S. In this case, the
scientist (in state |SOAm>) who is correlated to the object in
state |A>M is also correlated to the object in state |A>S,
which implies that the scientist is also in state |SOA> – i.e.,
she now lives in a universe in which object O was localized at AS at
t1 and she will not measure or observe anything in conflict with
that fact. Thus, if preexisting
correlations between M and S are such that |A>M ≈ |A>S
and |B>M ≈ |B>S, then S is not separable from M and
O at t1 because the event that correlates the positions of M and O
will simultaneously correlate the positions of S and O. Therefore, once the positions of M and O have
been correlated, there is no time period – not just a small time, but zero time
– in which S is separable and can measure M or O in a superposition.
An alternative explanation is this. The correlation event at t1 brings
into existence |A>M alongside |MOA> (as well as |B>M
alongside |MOB>). But because
|A>M ≈ |A>S and |B>M ≈ |B>S
, both |A>S and |B>S are also inevitably brought
into existence. But |A>S
is a state of object O that is located at AS relative to S; if it
exists, then there must be a corresponding scientist state |SOA>
that would measure O at AS.
Prior to the correlating event at t1, the
states of object O and device M could have been written, mathematically, in
uncountably different ways depending on the chosen basis, but that freedom
disappears upon the basis-determining correlation event. The basis of measurement is what calls into
existence the various possible states of O and M. The only question is whether that correlating
event can affect the existence of possible states of other objects to which M
is already correlated. I think the
answer is clearly yes: if a correlating event can call into existence state |A>M,
which implies the existence of correlated state |MOA>, and if |A>M
≈ |A>S, does this not also imply the existence of correlated
state |SOA>? In light of
the above analysis, Eq. 3 is corrected as follows:
Corrected Equation 3:
t0: (|A>S
+ |B>S) |M> |S> ≈ (|A>M + |B>M)
|M> |S>
= (|A>M + |B>M)
(|MOA> + |MOB>) (|SOAm> + |SOBm>)
t1 (event correlating positions of O and M): (|A>M |MOA> + |B>M |MOB>) (|SOAm>
+ |SOBm>)
= |A>M |MOA>
|SOAm> + |B>M |MOB> |SOBm>
≈ |A>S |MOA>
|SOA> + |B>S |MOB> |SOB>
t1+Δt: |A>S
|MAOA> |SOA> + |B>S |MBOB>
|SOB>
t2: |A>S
|MAOA> |SAOA> + |B>S
|MBOB> |SBOB>
So what’s wrong with Eqs. 1 and 3? It’s simple.
They fail to consider the effect of preexisting correlations between
systems. By assuming that O does not
correlate with S at t1 (allowing O and M to exist in superpositions
relative to S until t2), it follows that M cannot correlate to S,
which is possible only if |A>M ≠ |A>S at t1.
But not only is this a physically impossible evolution if |A>M ≈
|A>S at t0, it implies that the measuring device M
didn’t (and therefore cannot) succeed.
Said differently: If device M measures O relative to S, then Eq. 1 is
wrong at t1 (because the correlation with S would be simultaneous
and therefore S can’t show superposition), but if device M does not
measure O relative to S, then Eq. 1 is wrong at t2 because S does
not get correlated to O’s location relative to him (and the device M is
useless).
The problem with Eqs. 1 and 3 is that they assume that
S’s observation of M’s macroscopic pointer state at t2 is the event
that correlates S with O. That
assumption is indeed the very justification for SC, because it allows a nonzero
time period (t2 – t1) in which a cat, whose fate is
correlated to some quantum event, exists (and can in principle be measured) in
a superposition state relative to an external observer. If the observer remains uncorrelated to the
outcome of the quantum event until after observing the cat is its “macroscopic
pointer state” of |dead> or |alive>, then the observer can (in principle)
show SC in a superposition over these two states prior to his observation. But as we can see in the above Corrected Eq.
3, the event correlating the positions of O and S – which is the same one
correlating the positions of O and M – is independent of M’s future macroscopic
pointer state and whether or not S observes it.
F. Contradictions
Abound
I have argued above that the statement, “M measured the
position of O at t1,” only has meaning if it also correlates the
scientist (and any other observer) to a world in which the object is measured
at position AM (or one in which the object is measured at BM). And because positions relative to M are so
well correlated to positions relative to S (and every other large object), the
statement “The positions of M and O are correlated at t1”
necessarily implies “The positions of S and O are correlated at t1.” There is no time period after t1
in which O or M are (or can be demonstrated) in a superposition relative to
her. In Corrected Eq. 3, I have argued
that the correlation event between M and O also correlates S to O by creating
states |SOAm> and |SOBm> so as to produce entangled
state |A>M |MOA> |SOAm> + |B>M
|MOB> |SOBm>, and that in this state |S> appears
to be inseparable.
Despite my analysis in the previous sections, devout
adherents of the assumption of U (and the in-principle possibility of creating
SC, for example) are unlikely to be swayed and will insist that |S> is
separable at t1. So let me
accommodate them. What would be required
to maintain |S> as separable at t1 to ensure that S can measure O
and M in a superposition? Easy! Just set up the experiment so that |A>M
= |B>M. That would yield a
combined state in which |S> is certainly separable, but it is also one in
which device M didn’t actually measure anything. So, starting from a situation in which “M
measured the position of O at t1,” in which case scientist S becomes
simultaneously entangled to O by nature of that measurement, all we must do to
ensure the separability of S is to change the world so that it is not the case
that “M measured the position of O at t1.” In a very real sense, the only way to
separate |S> from the entangled state caused by the correlation event
between M and O is to retroactively undo that correlation event. In other words, the statement “M measured O
at t1” implies a correlation with S that renders it inseparable, unless
we are able to “undo” (or make false) the statement.
And lest I be accused of arguing tongue-in-cheek, let me
point out an intriguing fact about U, nearly absent from the academic
literature. Ultimately, for S to measure the correlated system M/O in a
superposition relative to her, she must measure it in an appropriate basis that
would reveal interference effects. Crucially,
the measurement process in that basis is one that would by necessity reverse
the process that correlated M and O and would thus “undo” the correlation. For instance, when someone asserts that SC
can be created and measured in an appropriately designed interference
experiment, such an experiment is necessarily one that would “turn back the
clock” and undo every correlation event.
Let’s forget for a moment how ridiculously
technologically difficult it would be to perfectly time-reverse all the
correlating events inside the SC box. Here
is a much bigger problem. If we open the
box and look – that is, measure the cat in basis {|dead>,|alive>} – we
will never obtain evidence that the cat (or the system including the cat) was
ever in a superposition. But if we
somehow succeed in measuring the system in a basis that would reveal
interference effects, then it will retroactively undo every correlation and
un-fact-ify every fact that could potentially evidence the existence of a cat
in state |dead> + |alive>. So in
neither case is there, or can there be, any scientific data to assert that SC
is an actual possibility (which follows from the inference of U). SC cannot be empirically confirmed because
any measurement that could demonstrate the necessary interference effects is
one that retroactively destroys any evidence of SC. On this basis alone, the assertion that SC is
a physically real possibility, which follows from the assumption of U, is
simply not scientific. Let me
elaborate. Consider this statement:
Statement Cat: “The measurement at time t1
of a radioactive sample correlates to the integrity of a glass vial of poison
gas, and the vial’s integrity correlates at time t2 to the survival
of the cat.”
Let’s assume this statement is true; it is a fact; it has
meaning. A collapse theory of QM has no
problem with it – at time t1, the radioactive sample either does or does
not decay, ultimately causing the cat to either live or die. According to U, however, this evolution leads
to a superposition in which cat state |dead> is correlated to one term and
|alive> is correlated to another.
Such an interpretation is philosophically baffling, leading countless
students and scholars wondering how it might feel to be the cat or, more
appropriately, Wigner’s Friend. Yet no
matter how baffling it seems, proponents of U simply assert that a SC superposition
state is possible because, while technologically difficult, it can be
demonstrated with an appropriate interference experiment. However, as I pointed out above, such an
experiment will, via the choice of an appropriate measurement basis that can
demonstrate interference effects, necessarily reverse the evolution of
correlations in the system so that there is no fact at t1 (to the
cat, the external observer, or anyone else) about the first correlation event
nor a fact at t2 about the second correlation event. In other words, to show that U is true (or,
rather, that the QM wave state evolves linearly in systems at least as
large as a cat), all that needs to be done is to make the original statement
false:
1) Statement
Cat is true;
2) U is
true;
3) To show U
true, Statement Cat must be shown false.
4) Therefore,
U cannot be shown true.
This is nonsense. To
summarize: U is not directly supported by empirical evidence but is rather an
inference from data obtained from microscopic systems. The inference of U conflicts with empirical
observations of macroscopic systems, giving rise to the measurement problem and
subjecting the inference of U to a higher standard of proof, the burden of
which lies with its proponents and remains unmet. However, the nature of the physical world
seems to enforce a kind of asymptotic size limit above which interference
experiments, and verification of U in the realm in which it causes the
measurement problem, seem FAPP impossible.
I argued in Section II(d) that this observation serves as evidence against
an inference of U, providing a further hurdle to the proponent’s currently
unmet burden of proof.
I then provided several novel logical arguments in
Section III showing why preexisting entanglements between a scientist and
measuring device guarantee that a measurement correlating the positions of the
device and an object in superposition simultaneously correlate the positions of
the scientist and the object. As a
result, there is no time at which the device is or can be measured in a
superposition relative to the scientist, in which case U is false because there
are at least some macroscopic superpositions, such as SC and WF, that cannot be
verifiably produced, even in principle. Further,
I showed that even if such an interference experiment could be done, such an
experiment would, counterintuitively, not show U to be true. That is because if U is true then it applies
to a statement about a series of events (measurements, correlations, etc.), but
showing that U applies to that statement requires showing that statement to be
false. This contradiction confirms that
U cannot, even in principle, be verified.
The final point I’d like to bring up is this. Undoing a correlation between two atoms that
are not themselves well correlated to other objects in the universe may not be
technologically difficult. The
statement, “Two atoms impacted at time t1” only has meaning to the
extent there is lasting evidence of that impact. An experiment or process that time-reverses
the impact can certainly undo the correlation, but then there is just no fact (from
anyone’s perspective) about the original statement. Quantum eraser experiments (e.g., Scully and
Drühl (1982) and Kim et al. (2000)) are intriguing examples of this.
However, everything changes for macroscopic objects;
cats, stars, and dust particles are already so well correlated due to past
interactions that trying to decorrelate any two or more such objects is
hopeless. Perhaps the analysis of
Section III can be boiled down to something like, “Preexisting correlations
between M and S, which are large objects with insignificant relative coherence
lengths, prevent M from ever existing or being measured in superposition
relative to S. When M correlates to O,
it does not inherit the superposition of O independently of S (as suggested by
linear dynamics); rather, S correlates to O simultaneously and transitively
with M.”
Due to this transitivity of correlation, universal
entanglement pervades the universe. Everything
is correlated with everything else and any experiment that aims to demonstrate
a cat in quantum superposition by measuring it in a basis that decorrelates it
from other objects is doomed to fail, not merely as a practical matter but in
principle. Even if there were a way to
undo the correlations between the cat, the vial of poison, and the
radioisotope, this could only be done by someone who was not already well correlated
to the cat and who could manage to remain uncorrelated to it during the
experiment. This, in light of the prior
analysis, is so ridiculously untenable that it warrants no further discussion.
REFERENCES
Aaronson,
S., Atia, Y. and Susskind, L., 2020. On the Hardness of Detecting Macroscopic
Superpositions. arXiv preprint arXiv:2009.07450.
Aharonov, Y.
and Kaufherr, T., 1984. Quantum frames of reference. Physical Review D, 30(2), p.368.
Albrecht, A.
and Phillips, D., 2014. Origin of probabilities and their application to the
multiverse. Physical Review D, 90(12), p.123514.
Deutsch, D.,
1985. Quantum theory as a universal physical theory. International Journal of Theoretical Physics, 24(1), pp.1-41.
Giacomini,
F., Castro-Ruiz, E. and Brukner, Č., 2019. Quantum mechanics and the covariance
of physical laws in quantum reference frames. Nature communications, 10(1), pp.1-13.
Goldstein,
S., 1987. Stochastic mechanics and quantum theory. Journal of Statistical Physics, 47(5-6), pp.645-667.
Kim, Y.H.,
Yu, R., Kulik, S.P., Shih, Y. and Scully, M.O., 2000. Delayed “choice” quantum
eraser. Physical Review Letters, 84(1), p.1.
Loveridge,
L., Busch, P. and Miyadera, T., 2017. Relativity of quantum states and
observables. EPL (Europhysics Letters), 117(4), p.40004.
Rovelli, C.,
1996. Relational quantum mechanics. International Journal of Theoretical Physics, 35(8), pp.1637-1678.
Scully, M.O. and Drühl, K., 1982. Quantum eraser: A proposed photon correlation
experiment concerning observation and" delayed choice" in quantum
mechanics. Physical Review A, 25(4), p.2208.
Zych, M.,
Costa, F. and Ralph, T.C., 2018. Relativity of quantum superpositions. arXiv preprint arXiv:1809.04999.
We view the world as eigenstates of observables, so
if Strong Relativity is correct, then so must the cat. There is nothing special in this example
about choosing the live cat’s perspective.
From the perspective of the dead cat, the lab is in the following
equally ridiculous superposition: |lab that would measure a dead cat, which
isn’t surprising, because it is dead> + |lab that is so distorted, whose
measuring devices are so defective, whose scientists are so incompetent, that
it would measure a dead cat as alive>.
The point of this example is to show that the impossibility of SC
follows almost tautologically from the Strong Relativity of quantum
superpositions.
|A>M ≈ |A>S, for
instance, does not say that location A is the same distance from M as from
S. Rather, it says that location A
relative to M is well correlated to location A relative to S; there is zero (or
inconsequential) quantum fuzziness between the locations; M and S see point A
as essentially the same location.
To clarify: if the object’s state is |A>S
at t0, then physical evolution of the object over time limits where
the object might be found in the future, such that scientist S in state |SOA>
will never find object O at a location that is logically inconsistent with its
state |A>S at t0.
For instance, if measurement event correlates the
momenta of O and M instead of position, then the term |B>S |SOA>
will not, as a mathematical matter, disappear, but only because it can be
written as a series of terms that includes, among others: |object has momentum
P> |scientist will not measure object’s momentum other than P>, where P
is some semiclassical momentum eigenstate.
Of course, I can certainly show, empirically, that
Statement Cat is true, simply by setting up the experiment and watching it
progress.