Linear/Unitary Quantum Mechanics Cannot Apply Universally

In my last post, I provided several arguments why the inference of U is logically invalid.  As a quick rehash, many (perhaps most) of the big problems in foundational physics arise from an assumption (“U”) that the quantum mechanical wave function always evolves linearly or unitarily, so that when a small object in quantum superposition interacts with a large system, the large system “inherits” the superposition.  Because U asserts that this is always true, no matter how big the system, then cats (like Schrodinger’s Cat) and people (like Wigner’s Friend) can exist in weird macroscopic superposition states.  This is a problem because, well, we never observe cats or anything else in superposition in our ordinary lives!  There are lots more problems and weird implications that follow from U, so it’s amazing just how few people have (at least in the academic literature) questioned U. 

Today’s post is my attempt to actually disprove U.  I use a variety of novel logical arguments to show that U is actually false -- or, at least, empirically unverifiable, which would place it outside the realm of science.  Together, these posts will be put together and submitted as a journal article even if that minimal effort is unrewarded. 

III.       A NEW LOGICAL ARGUMENT AGAINST U

In Section II, I attempted to show that U is not scientifically justified as a valid inference because relevant empirical evidence supports only ¬U.  In this section, I will present a new logical argument attempting to show an example in which U cannot be experimentally verified even in principle.  In other words, not only does U lack experimental verification, I will argue that U cannot be experimentally verified.  I will first discuss the nature of a quantum superposition from a logical standpoint, then address the extent to which quantum superpositions must be relative.  Finally, I will present three variations on the argument.

A brief caveat: this argument is more likely to benefit the skeptics of U than of its devoted adherents.  Consider this statement: “A scalable fault-tolerant quantum computer can be built.”  Let’s assume for the moment that it is in fact false, and could logically be shown to be false because of some inconsistency with other facts about the universe, but happens to be empirically unfalsifiable.  Those who are already convinced that the statement is true will be unlikely to be persuaded by a priori logical argumentation.  If they are in the field of quantum computing, they may be responsible for directing private and public funding toward achievement of a fundamentally unfulfillable goal.  Waiting either for success or empirical falsification, they continue to throw good money after bad, depriving more viable scientific goals of funding.

Such is the case with the assumption of U.  If U is in fact false, but turns out to be empirically unfalsifiable, then any logical argument against U will probably not be compelling to anyone who is already convinced of U.  Instead, the following arguments are probably most accessible and relevant to those scientists who are already skeptical of U.  Throughout the following analyses, I will simply assume U true and show how that assumption leads to logical problems.

A.        What is a Quantum Superposition?

Let’s return to the double-slit interference experiment in which a particle passes through a plate having slits A and B and assume that the experiment is set up so that the wave state emerging from the plate is (unnormalized) state |A> + |B>.  What does that mean?  |A> represents the state the particle would be in if it were localized in slit A, while |B> represents the state the particle would be in if it were localized in slit B.  If the particle had been in state |A>, for example, then a future detection of that particle would be consistent with its having been localized in slit A.[1] 

However, superposition state |A> + |B> is not the same as state |A>.  In other words, state |A> + |B> is not the state of the particle localized in slit A, nor is it the state of the particle localized in slit B.  However, it is also not the state of the particle not localized in slit A (because if it were not in A, it would be in B), nor is it the state of the particle not localized in slit B.  Therefore, for a particle in state |A> + |B>, none of the following statements is true:

·         The particle is in slit A;

·         The particle is not in slit A;

·         The particle is in slit B;

·         The particle is not in slit B.

While these statements may seem contradictory, the problem is in assuming that there is some fact about the particle’s location in slit A or B.  Imagine two unrelated descriptions, like redness (versus blueness) and hardness (versus softness).  “Red is hard” and “red is soft” might seem like mutually incompatible statements, one of which must be true and the other false, but of course they are nonsensical because there just is no fact about the hardness of red, or the redness of soft, etc.  Analogously, for a particle in state |A> + |B>, there just is no fact about its being localized in slit A or B.  The problem is in assuming that “The particle is in slit A” is a factual statement – that there exists a fact about whether or not the particle is in slit A.  Unfortunately, the assertion that there exists such a fact is itself incompatible with the particle being in state |A> + |B>.

Note also that state |A> + |B> is not a representation of lack of knowledge; it does not mean that the state is actually |A> or |B> but we don’t know which, nor does it have anything to do with later discovering, via measurement, which of state |A> or |B> was correct.  If an object is in fact in a superposition state now, a future measurement does not retroactively change that fact.  (See, e.g., Knight (2020).) 

If an object is in state |A> + |B>, then there just is no fact about its being in state |A> or |B> – not that we don’t know, not that it is unknowable, but that such a fact simply does not exist in the universe.  This counterintuitive notion inevitably leads many to confusion.  After all, if a cat could exist in state |alive> + |dead>, and if that state is properly interpreted as there being no fact about its being alive or dead, what does that say about the cat?  Wouldn’t the cat disagree?  And what quantum state would the cat assign to you?   Of course, if SC turns out to be impossible to create, even in principle, then these worries disappear. 

B.        Relativity of Quantum Superpositions

In the above example, |A> represented the state the particle would be in if it were localized in slit A.  To be more technical, |A> is an eigenstate of the position operator corresponding to a semiclassical localization at position A.  But where exactly is “position A”?  If there is one thing that Galileo and Einstein collectively taught us, it’s that positions (among other measurables) are relative.  That recognitional already instructs us that state |A> + |B> is meaningless without considering that the locations of positions A and B are relative to other objects in the universe.  In other words, quantum superpositions are inherently relative.  There are two types of relativity of quantum superpositions I’ll discuss:

·         Weak Relativity of quantum superpositions: Measurement outcomes (eigenstates of an observable) are relative to other measurement outcomes. 

·         Strong Relativity of quantum superpositions: Essentially an extension of Galilean and Einsteinian Equivalence Principles, Strong Relativity requires that if a first system (such as a molecule) is in a superposition from the perspective of a second system (such as a laboratory), then the second system is in a corresponding superposition from the perspective of the first system.  For instance, if a microscopic object is in a superposition of ten distinct momentum eigenstates relative to a measuring device, then the measuring device is conversely in a superposition of ten distinct momentum eigenstates relative to the microscopic object. 

While the notion of “quantum reference frames” is not new (Aharanov and Kaufherr (1984) and Rovelli (1996)), the above notion of Strong Relativity has only recently been discussed in the academic literature (Giacomini et al. (2019), Loveridge et al. (2017), and Zych et al. (2018)).  If it is true, then it’s relatively easy to show, as I did in this paper, that SC is a myth and that macroscopic quantum superpositions cannot be demonstrated in principle.  In a sense, the truth of Strong Relativity excludes the possibility of SC nearly as tautology, since if a lab from whose perspective a cat is in state |alive> + |dead> can equivalently be viewed from the perspective of the cat, then which cat?  And what quantum state would describe the lab from the cat’s perspective?  From the perspective of the live cat, perhaps the cat would view the lab in the superposition state:

|lab that would measure me (the cat) as live> + |lab that would measure me (the cat) as dead>

And if we think that cat states |alive> and |dead> are interestingly distinct, can you imagine how incredibly and weirdly distinct those eigenstates would seem from the perspective of the live cat?  Rewriting the above state with a little more description, the lab would appear from the live cat’s perspective as state:

|lab that would measure me (the cat) as live, which isn’t surprising, because I am alive> +

|lab that is so distorted, whose measuring devices are so defective, whose scientists are so incompetent, that it would measure me (the cat) as dead>

The second eigenstate is actually far worse than described.  Every single measurement made by that lab would have to correspond, from its perspective, to a dead cat; the scientists in it, when looking at the cat, when receiving and processing trillions of photons bouncing off the cat, would have to see a dead cat!  And it’s worse than that.  Even when the scientists leave the lab, the universe requires that the story stays consistent; no future fact about the lab, its measuring devices, or its scientists – or anything they interact with in the future – can conflict with their observation of a dead cat, even though that second eigenstate is from the perspective of a live cat![2]

I derived the notion of Strong Relativity independently and therefore regard it as nearly obviously true.  Nevertheless, because it is by no means universally accepted (or even known) by physicists or philosophers, I won’t depend on it in this paper.  Instead, I’ll use Weak Relativity, which is obviously and necessarily true.  For instance, a particle is only vaguely specified by state |A> + |B>.  For a scientist S in a laboratory L who plans to use measuring device M to detect the particle whose state |A> + |B> references positions A and B, we should be asking whether positions A and B are localized relative to the measuring device M, the lab L, the scientist S, etc.  In other words, is the particle in state |A>_M + |B>_M, |A>_L + |B>_L, or |A>_S + |B>_S?

Why does this matter?  Surely position A is the same position relative to the measuring device, lab, and scientist.  And for essentially all practical purposes, that’s true, which is probably why the following analysis is absent from the academic literature.  After all, how could the measuring device, scientist, etc., disagree about the location of position A? 

As discussed in Section II, quantum uncertainty disperses a wave packet, so over time a well-localized object tends to get “fuzzy” or less well localized.  Why don’t we notice this effect in our ordinary world?  What keeps the scientist from becoming delocalized relative to the lab and measuring device?  First, the effect is inversely related to mass.  We barely notice the effect on individual molecules, so we certainly won’t notice it with anything we encounter on a daily basis.  Second, events, such as impacts with photons, air molecules, etc., are constantly correlating objects to each other and thus decohering relative superpositions.  For example, the air molecules bouncing between the scientist and measuring device are constantly “measuring” them relative to each other, preventing their wave packets from dispersing relative to each other.     

So while the scientist might in principle be delocalized from the measuring device by some miniscule amount, that amount is much, much, much smaller than could ever be measured, and is therefore irrelevant to whether position A is located relative to the scientist S, the measuring device M, or the lab L.  Therefore, it’s usually fine to write state |A> + |B> instead of |A>_M + |B>_M, etc., because |A>_M + |B>_M ≈ |A>_L + |B>_L ≈ |A>_S + |B>_S.[3]

However, if U is true, then producing SC or WF (and correspondingly enormous relative delocalizations[4]) are actual physical possibilities, if perhaps very difficult or impossible to achieve in practice.  If we’re going to talk about cat state |alive> + |dead>, or a superposition of a massive object in position eigenstates so separated that they would produce distinct gravitational fields (Penrose (1996)), or macroscopic quantum superpositions in general, then we can no longer be sloppy about how (i.e., in relation to what) we specify a superposition of eigenstates.  That said, I’ll now argue how keeping track of these relations between systems implies that there are at least some macroscopic quantum superpositions (such as SC) that cannot be measured or empirically verified, even in principle.

C.        The Argument in Words

A scientist S (initially in state |S>) wants to measure the position of a tiny object O.  The object O is in a superposition[5] of position eigenstates corresponding to locations A and B, separated by some distance d, relative to the scientist S.  Neglecting normalization constants, |O> = |A>_S + |B>_S.  To measure it, he uses a measuring device M (initially in state |M>) configured so that a measurement of the position of object O will correlate device M and object O so that device M will then evolve over (some brief but certainly nonzero) time to a corresponding macroscopic pointer state, denoted |M_A> or |M_B>.  Device M in state |M_A>, for example, indicates “A” such as with an arrow-shaped indicator pointing at the letter “A.”  In other words, device M is designed/configured so that if M measures object O at location A, then M will, through a causal chain that amplifies the measurement, evolve to some state that is very obviously different to the scientist S than the state to which it would evolve had it measured object O at location B.  The problem, reflecting Weak Relativity, is that device M measures the location of object O relative to it.  Relative to device M, the object O is in state |A>_M + |B>_M, which means that a correlating event between O and M will cause M to evolve into a state in which macroscopically indicating “A” correlates to its measurement of the object at position A relative to M, and vice versa for position B.

Of course, this doesn’t typically matter in the real world.  The scientist S is already well localized relative to device M; there is essentially no quantum fuzziness between them.  Because |A>_M + |B>_M ≈ |A>_S + |B>_S, measurement of the object O at A relative to M is effectively the same as its measurement relative to S, so the device’s macroscopic pointer state will properly correlate to the object’s location at position A or B relative to S, which was exactly what the scientist wanted to measure.  However, under what circumstances would it matter whether |A>_M + |B>_M ≠ |A>_S + |B>_S, and how could this situation come to pass?

Let’s say that the experiment is set up at time t₀; then at time t₁ the device M “measures” the object O via some initial correlation event, after which M then evolves in some nonzero time Δt to a correlated macroscopic pointer state; and then at t₂ the scientist S reads the device’s pointer.

Under these normal circumstances, at time t₀, object O is in a superposition relative to both M and S.  (Said another way, relative to M and S, there is no fact at t₀ about the location of O at A or B.)  Its being in a superposition is what makes possible an interference experiment on O to demonstrate its superposition state.  Skipping ahead to time t₂, the scientist S is correlated to M and O – i.e., the object’s position at B, for example, is correlated with the device’s pointer indicating “B” and the scientist’s observation of the device indicating “B.”  At time t₂, object O is no longer in a superposition relative to either M or S.  (Said another way, relative to M and S, there is a fact at t₂ about the location of O at position A or B.)  Consequently, at t₂ it is not possible, even in principle, for the scientist S to do an interference experiment on object O or device M to demonstrate a superposition, because they aren’t.  It is not a question of difficulty; I am simply noting the (hopefully uncontroversial) claim that by time t₂, the position of object O is already correlated to that of the scientist S, so he now cannot physically demonstrate, via an interference experiment, that there is no fact about O’s location at A or B relative to him.

Let me summarize.  At t₀, object O is in a superposition relative to S, so scientist S could in principle demonstrate that with a properly designed interference experiment.  Device M, however, is well localized relative to S, so scientist S would be incapable at t₀ of showing M to be in a superposition.  At t₂, neither O nor M is in a superposition relative to S, so S obviously cannot perform an interference experiment to prove otherwise.  The only question remaining is: what is the state of affairs at time t₁ (or t₁+Δt)?[6]  The standard narrative in quantum mechanics, which follows directly from the assumption of U, is the following von Neumann chain:

Equation 1:

t₀:                     |O> |M> |S>

                        = (|A> + |B>) |M> |S>

t₁ (or t₁+Δt):    (|A> |M_A> + |B> |M_B>) |S>

t₂:                    |A> |M_A> |S_A> + |B> |M_B> |S_B>

According to Eq. 1, at time t₁ object O and device M are correlated to each other but scientist S is uncorrelated to O and M.  Said another way, O and M are well localized relative to each other (i.e., there is a fact about O’s location relative to M) but S is not well localized to O or M (i.e., there is not a fact about the location of O or M relative to S).  If that is true, then scientist S would be able, at least in principle, in an appropriate interference experiment, to demonstrate that object O and device M are in a superposition relative to him.  No one claims that such an experiment would be easy, but as long as there is some nonzero time period (in this case, t₂ - t₁) in which such an experiment could be done, then maybe it’s just a question of technology.  The problem, as I will explain below, is that there is no such time period.  The appearance of a nonzero time period (t₂ – t₁) in Eq. 1 is an illusion caused by failure to keep track of what the letters “A” and “B” actually refer to in each of the terms.

Let’s assume Eq. 1 is correct: that at time t₁, the location of O is correlated to M but is not correlated to S.  That means that the location at which M measured O, which is what determines the macroscopic pointer state to which M will evolve, is not correlated to the location of O relative to S.  Consequently, the macroscopic pointer state to which M will evolve will correlate to the location of O relative to M at t₁, but because that location of O (relative to M) is not correlated to its location relative to S, the macroscopic pointer state of M will itself be uncorrelated to O’s location relative to S.  Then, at t₂, S’s observation of M’s pointer will therefore be uncorrelated to O’s location relative to him. 

Let me reiterate.  Object O is in a superposition of position eigenstates |A>_S and |B>_S relative to scientist S.  He asks a simple question: “Will I find it in position A or B?”  To answer the question, he uses a measuring device M that is designed to measure the object’s position and indicate either output “A” or “B.”  But if Eq. 1 is correct, then when he looks at the device’s output, a reading of “A” does not tell him where the object was measured relative to him, which is what he was trying to determine!  Rather, the device’s output tells him where the object was measured relative to the device, to which, at time t₁, he was uncorrelated.

If Eq. 1 is correct at t₁ that M is in a superposition relative to S (by virtue of its entanglement with object O), then the device’s measurement and subsequent evolution are uncorrelated to the location of object O relative to scientist S.  In other words, if Eq. 1 is correct, then as far as scientist S is concerned, measuring device M didn’t measure anything at all.  Instead, the macroscopic output of the device M would only correlate to the object’s location relative to S if M was well correlated to S at time t₁, in which case Eq. 1 is wrong.

I should stress that the current narrative in physics is not just that Eq. 1 is possible, but that a comparable von Neumann chain occurs in every quantum mechanical measurement, big or small.  At t₁, device M, but not scientist S, is correlated to the position of object O.  But what I’ve just shown is that if that’s true, then the position of O to which M is correlated is a different position of O than the scientist S intended to measure, such that the device’s output will necessarily be uncorrelated – and thus irrelevant – to the scientist’s inquiry.  If Eq. 1 is correct – if macroscopic device M, which is correlated to object O, can be in a superposition relative to scientist S – then measuring devices aren’t necessarily measuring devices and the very foundations of science are threatened.

Conundrum as this may be, it’s not even the whole problem with Eq. 1.  We have to ask how it could be that the measuring device failed.  Remember that what the scientist wants to measure is the object in state |A>_S or |B>_S, but the device M is only capable of measuring the object in state |A>_M or |B>_M.  When he starts the experiment at t₀, he and device M are already well correlated, the presumption being that a measurement by the device of |A>_M, when observed by the scientist, will correlate to |A>_S.  But if Eq. 1 is correct, then the correlation event at t₁ is one that guarantees that this can’t happen, which means that at t₁, |A>_M ≠ |A>_S.  So even though |A>_M ≈ |A>_S at t₀, Eq. 1 implies that |A>_M ≠ |A>_S at t₁ (and by a significant distance).  That is, the quantum fuzziness between device M and scientist S (both macroscopic systems) would have to grow from essentially zero to a dimension comparable to the distance d separating locations A and B.  The analysis in Section II, particularly regarding relative coherence lengths and wave packet dispersion, shows that such a growth over any time period, and certainly the short period from t₀ to t₁, is impossible in principle.

Let me paraphrase.  At t₁, device M has measured object O relative to it, so there is a fact about O’s location relative to M.  But if we stipulate as in Eq. 1 that there is not a fact about O’s location relative to S (by claiming that it’s still in a superposition relative to S), then what M has measured as position A (|A>_M) might very well correspond to what S would measure as position B (|B>_S) – or more generally, M’s indicator pointer will not correlate to O’s location relative to S.  That just means that, at t₁, M did not measure the location of O relative to S.  The only way this could have happened is if |A>_M and |A>_S, which were well correlated at time t₀, had already become adequately uncorrelated via quantum dispersion by time t₁.  This is physically impossible.  Therefore Eq. 1 is incorrect: at no point can scientist S measure device M in a superposition.

D.        The Argument in Drawings

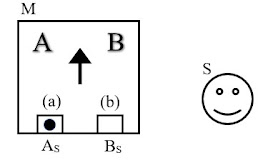
In this section, I’ll provide a comparable logical argument with reference to drawings.  In Fig. 1a, object O is shown at time t₀ in a superposition of position eigenstates corresponding to locations at A_S and B_S relative to scientist S, where the object O is shown crosshatched to represent its superposition, relative to S, over two locations.  Measuring device M has slots (a) and (b) and is configured so that detection of object O in slot (a) will, due to a semi-deterministic causal amplification chain, cause device M to evolve over nonzero time Δt to a macroscopic pointer state in which a large arrow indicator points to the letter “A,” and vice versa for detection of object O in slot (b).  Because the device’s detection of object O in slot (a) actually corresponds to measurement of the object O at location A_M relative to M (and vice versa for slot (b)), the device M is placed at time t₀ so that A_M ≈ A_S and B_M ≈ B_S for the obvious reason that the scientist S intends to measure the object’s location relative to him and therefore wants the device’s indicator to correlate to that measurement.  Finally, the experiment is designed so that the initial correlation event between object O and device M occurs at time t₁, device M evolves to its macroscopic pointer state by time t₁+Δt, and scientist S reads the device’s pointer at t₂.

Fig. 1a

Figs. 1b and 1c show how the scientist might expect (and would certainly want) the system to evolve.  In Fig. 1b, the locations of O relative to M and S are still well correlated (i.e., A_M ≈ A_S and B_M ≈ B_S), so the device’s detection of object O in slot (a) correlates to the object’s location at A_S.[7]  Then, in Fig. 1c, device M has evolved so that the indicator now points to letter “A,” correlated to the device’s detection of object O in slot (a).  Then, when scientist S looks at the indicator at time t₂, he will observe the indicator pointing at “A” if the object O was localized at A_S and “B” if it was localized at B_S, which was exactly his intention in using device M to measure the object’s position.

         

Fig. 1b                                                             Fig. 1c

Notice, however, that at time t₁ the object O is not in a superposition relative to S, nor is device M (which is correlated to object O).  At t₁, object O is indeed localized relative to device M, and since A_M ≈ A_S and B_M ≈ B_S, it is localized relative to scientist S.  We don’t know, of course, whether object O was detected in slot (a) or (b), and Fig. 1b only shows the first possibility, but it is in slot (a) or (b) (with probabilities that we can calculate using the Born rule), with slot (a) correlated to A_S (which is localized relative to S) and slot (b) correlated to B_S (which is also localized relative to S).  If that weren’t the case, then object O’s position would still be uncorrelated to device M, which negates the correlation event at t₁.  In other words, at time t₁ in Fig. 1b, object O is localized at A_S or B_S – i.e., there is a fact about its location relative to S – whether or not S knows this.[8]  Because object O is localized relative to S at t₁, S cannot do an interference experiment to show O in superposition, nor can S show device M, which is correlated to O, in superposition.

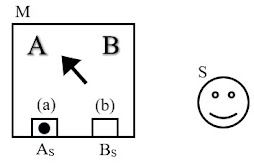
Now, suppose we demand, consistent with Eq. 1, that at time t₁, scientist S can, in principle, with an appropriately designed interference experiment, demonstrate that object O and device M are in a superposition (relative to S).  That requirement implies that the object’s location, as measured by M via the correlation event at t₁, does not correlate to the object’s location relative to S.  The device’s detection at t₁ of the object O in, for example, slot (a), which corresponds to its measurement of the object at A_M, cannot correlate to the location of the object at A_S – otherwise S would be incapable of demonstrating O (or M, to which O is correlated) in superposition.  Thus, to ensure that object O remains unlocalized relative to S when the correlation event at t₁ localizes object O relative to M, that location which M measures as A_M by detection of object O in slot (a) cannot correlate to location A_S. 

Fig. 2a

This situation is shown in Fig. 2a in which both object O and device M are shown in a superposition of position eigenstates relative to S.  The object’s crosshatching, as in Fig. 1a, represents its superposition, relative to S, over locations A_S and B_S.  Analogously (but without crosshatching), device M localized at M_A is shown superimposed on device M localized at M_B.  Importantly, M_A is the position of device M that would measure the position of object O at A_M (by detecting it in slot (a)) as A_S, while M_B is the position of device M that would measure the position of object O at A_M (by detecting it in slot (a)) as B_S.  Because O remains uncorrelated to S at t₁ (as demanded by Eq. 1), the measuring device M that detects O in slot (a) must also be uncorrelated to S at t₁.  Again, the same is true for device M that detects O in slot (b), which is not shown in Fig. 2a.  What is demonstrated in Fig. 2a is that the correlation event at t₁ between device M and object O that localizes O relative to M requires that M is not correlated to S, thus allowing S to demonstrate M in a superposition, as required by Eq. 1.  Then, in Fig. 2b, at time t₁+Δt, device M has evolved so that the indicator now points to letter “A,” correlated to the device’s detection of object O in slot (a). 

Fig. 2b

 

However, now we have a problem.  In Fig. 2b, the pointer indicating “A,” which is correlated to the device’s localization of object O at A_M, is not correlated to the object’s localization at A_S.  When the scientist S reads the device’s indicator at time t₂, it is not that the output is guaranteed to be wrong, but rather that the output is guaranteed to be uncorrelated to the measurement he intended to make.  Worse, it’s not just that the output is unreliable – sometimes being right and sometimes being wrong – it’s that the desired measurement simply did not occur.  The correlation event at time t₁ did not correlate the scientist to the object’s location relative to him.

Therefore, to guarantee that object O (and device M, to which it is correlated) is in superposition relative to scientist S at t₁, as required by Eq. 1, the location A_M as measured by device M cannot correlate to location A_S relative to scientist S; thus there is no fact at t₁ about whether the measurement at A_M (which will ultimately cause device M to indicate “A”) will ultimately correlate to either of locations A_S or B_S relative to S.  (Similarly, there is no fact at t₁ about whether location B_M will correlate to either A_S or B_S.)  That is only possible if that location which device M would measure at t₁ as A_M could be measured by scientist S as either A_S or B_S, which is only possible if A_M ≠ A_S.

To recap: At t₀ the scientist S sets up the experiment so that A_M ≈ A_S and B_M ≈ B_S, which is what S requires so that measuring device M actually measures what it is designed to measure.  If Eq. 1 is correct, it implies that at time t₁, A_M ≠ A_S and B_M ≠ B_S.

This has two consequences.  First, we need to explain how (and whether) device M could become adequately delocalized relative to scientist S so that A_M ≠ A_S and B_M ≠ B_S in the time period from t₀ to t₁.  Remember, we are not talking about relative motion or shifts – we are talking about A_M and A_S becoming decorrelated from each other so as to be in a location superposition relative to each other.  In other words, how do A_M and A_S, which were well localized relative to each other at time t₀, become so “fuzzy” relative to each other via quantum wave packet dispersion that A_M ≠ A_S at time t₁?  They don’t.  As long as the relative coherence length between two objects is small relative to the distance d separating distinct location eigenstates, then the situation in which A_M ≠ A_S cannot happen over any time period. 

Second, the quantum amplification in a von Neumann chain depends on the ability of measuring devices to measure what they are intended to measure.  A state |A>_S + |B>_S can only be amplified through entanglement with intermediary devices if those terms actually become correlated to states |A>_S and |B>_S, respectively.  But if, as required by Eq. 1, there is some nonzero time period (t₂ - t₁) in which scientist S could in principle measure M and O in a superposition, then the device’s measurement of the object’s location relative to it cannot correlate to the object’s location relative to S, in which case future states of S cannot be correlated to either |A>_S or |B>_S.  Eq. 1 is internally inconsistent and is therefore false.  There is no time period in which scientist S can measure M and O in a superposition.

E.        The Argument in Equations

A quick warning: as discussed in Section II(b), the QM mathematical formulism is the cause of the measurement problem and inherently cannot be part of the solution.  The problem with Eq. 1, which follows directly from U and has been shown to be problematic in the previous sections, will not be apparent by using the traditional tools and equations available in QM.  In the following analysis I will explain and adopt a new nomenclature that I hope will be helpful in relaying the arguments of the prior sections. 

Another quick warning.  The assumption that SC and WF, for example, are experimentally possible in principle depends on the ability of an external observer to subject them to a “properly designed interference experiment,” which is one in which the chosen measurement basis is adequate to reveal interference effects between the separate terms of the superposition.  No one denies that the required measurement basis for revealing a cat in superposition over |dead> and |alive> states would be ridiculously complicated and extremely technologically challenging.[9]  However, there are some, such as Goldstein (1987), who claim that every measurement is ultimately a position measurement.  If so, then no experiment could ever demonstrate a complicated macroscopic quantum superposition like SC.  Further, as I’ll discuss in more detail in Section F, the measurement basis required to demonstrate SC is also one that guarantees that SC does not exist, leading to a contradiction that, I will argue, renders moot any seeming logical paradox.

Regarding nomenclature: by state |A>_S, I mean the state of an object O that is located at position A relative to the scientist S, by which I mean a state in which there is a fact about its location relative to S, whether or not S knows it.  And what does that mean?  It means that if O is in state |A>_S at time t₀, then S will not, after t₀, make any measurements, have any experiences, etc., that are inconsistent with that fact or even, more importantly, any of its consequences.  And that certainly includes interference experiments.  Because |A>_S is a state of object O located at position A relative to scientist S, it implies a state of the scientist S that is correlated to the location of O at position A relative to him.  The scientist S in that state, which I’ll write |S^OA>, may or may not ever measure the location of object O, but if he does, he will with certainty find object O at position A (or somewhere that is logically consistent with the object having been located at position A when the object was in state |A>_S).[10]  Said differently, |A>_S is a state of object O in which scientist S would be incapable of measuring O in orthogonal state |B>_S, state |A>_S + |B>_S, or any future state logically inconsistent with |A>_S.

For instance, imagine if whether it rains today hinges on some quantum event that is heavily amplified, such as by chaotic interactions.  (Indeed, Albrecht and Phillips (2014) brilliantly argue that all probabilistic effects, certainly including weather, are fundamentally quantum.)  Specifically, imagine that a tiny object, located in Asia and in spin superposition |up> + |down>, was “measured” by the environment in the {|up>,|down>} basis by an initial correlating interaction or event, followed by an amplification whose definite mutually exclusive outcomes, correlated to the object’s measurement as “up” or “down,” are that it either will or will not, respectively, rain today in Europe.  If that object were in fact in state |up>, in which case it will rain today in Europe, then no observer would make any measurements or have any observations that are inconsistent with that fact.  Of course, the observer in Europe would not immediately observe that fact or its consequences, but once the fact begins to manifest itself in the world, that observer will eventually observe its effects – notably rain.  That observer – the one correlated to observing rain – now lives in a universe in which he will not and cannot make a contradictory observation (i.e., one logically inconsistent with the fact of |up> or its consequences).

Of course, a superposition is fundamentally different.  For an object in state |A>_S + |B>_S, there is no fact about the object’s location at position A or B relative to scientist S.  While |A>_S is a state in which O is in fact located at A relative to S, which implies that S is in state |S^OA> that is correlated to the location of O at position A relative to him, it is a mistake to assume that |S^OA> exists without |A>_S – i.e., it is a mistake to assume that they are already correlated prior to a correlating or entangling event.  After all, prior to a correlation event, the state of S can mathematically be written in lots of different bases, most of which would be useless or irrelevant.  Even though it may be correct that an object O is in state |A>_S + |B>_S, that same superposition can be written in different measurement bases, and the state in which O will be found upon measurement will depend on the relevant measurement basis.  So just as O can be written in state |A>_S + |B>_S (among others) and S can be written in state |S^OA> + |S^OB> (among others), neither |A>_S nor |S^OA> come into being until, in this case, a position measurement correlates them.  Before the correlation event, there is no object O in state |A>_S just as there is no scientist S in state |S^OA>, while after the correlation event there is.

Let me elaborate.  If object O is in state |A>_S + |B>_S, then it is in fact not in either state |A>_S or |B>_S, which also means that the scientist S is not in state |S^OA> or |S^OB>.  Remember that the scientist in state |S^OA>, if he measures object O, will with certainty find it at position A.  But if object O is in fact in state |A>_S + |B>_S, there is no such scientist.  That the state of O can be written as |A>_S + |B>_S implies that the state of S can be written as |S^OA> + |S^OB>.  Just as object O is in neither state |A>_S nor |B>_S (or, stated differently, there is no object O in state |A>_S or |B>_S) and there is therefore no fact about its location at A or B relative to S, we can also say that scientist S is in neither state |S^OA> nor |S^OB> and there is no fact about whether he would with certainty find O at position A or B.  Until a measurement event occurs between O and S that correlates their relative positions, there is no scientist S that would with certainty find object O at A (or B), just as there is no object in state |A>_S or |B>_S.  It’s not an issue of knowing which state the scientist is in, for if S were actually in |S^OA> or |S^OB> but did not know which, then he was mistaken about being in state |S^OA> + |S^OB>.  That is, before the correlation event, there is no scientist in state |S^OA> or |S^OB>.  Rather, what brings states |S^OA> and |S^OB> (as well as |A>_S and |B>_S) into existence[11] is the event that correlates the relative positions of S and O:

Equation 2:

t₀:         |O> |S> = (|A>_S + |B>_S) |S> = (|A>_S + |B>_S) (|S^OA> + |S^OB>)

            = |A>_S |S^OA> + |B>_S |S^OA> + |A>_S |S^OB> + |B>_S |S^OB>

t₂ (event correlating their positions): |A>_S |S^OA>  + |B>_S |S^OB>

Note that at time t₀, the scientist in state |S> is still separable (i.e., unentangled) with |O> and can, in principle, demonstrate O in a superposition relative to him.  However, the correlation event at t₂ entangles S with O so that no scientist (whether in state |S^OA> or |S^OB>) can measure O in a superposition.  Mathematically, the correlation event eliminates incompatible terms, leaving only state |S^OA> correlated to |A>_S and state |S^OB> correlated to |B>_S.  States |B>_S and |S^OA>, for example, are only incompatible from the perspective of position measurement.  If the correlation event is one that measures O in a different basis, then each of |B>_S and |S^OA> can be written in that basis and the correlation event caused by the measurement will not necessarily eliminate all terms.[12]  This point further underscores that writing the state of S as |S^OA> + |S^OB>, and its expansion in Eq. 2, are purely mathematical constructs until the event at t₂ that correlates the positions of O and S brings |S^OA> and |S^OB> into existence and allows us to eliminate incompatible terms.

Let’s return to the original example in which scientist S utilizes intermediary device M at time t₁ to measure the position of object O relative to him, which is initially in state |A>_S + |B>_S.  Of course, Weak Relativity requires that device M is only capable of measuring positions relative to it, but scientist S has set up the experiment so that at time t₀, |A>_M ≈ |A>_S and |B>_M ≈ |B>_S.  In the following nomenclature, |M^OA>, for example, is a state of device M correlated to localization of object O at position A_M (relative to M).  M in state |M^OA> can certainly try to measure O in a basis other than position, but the existence of M in state |M^OA> implies that O has already been localized at A_M so that the outcome of a subsequent measurement will not be inconsistent with its initial localization at A_M.  It is important to note that |M^OA> is not itself a macroscopic pointer state; rather, assuming device M is designed correctly[13], |M^OA> is a state that cannot evolve to a macroscopic pointer state correlated to object O located at B_M.  In other words, a macroscopic pointer state of M indicating “A” will be correlated to |M^OA> and not |M^OB>.  Therefore, I’ll write that pointer state, which evolves from state |M^OA> over nonzero time Δt, as |M_A^OA>.  Using this nomenclature, we can expect, according to the assumption of U, the following von Neumann-style measurement process:

Equation 3:

t₀:         (|A>_S + |B>_S) |M> |S> ≈ (|A>_M + |B>_M) |M> |S>

= (|A>_M + |B>_M) (|M^OA> + |M^OB>) (|S^OA> + |S^OB>)

t₁ (event correlating positions of O and M):   (|A>_M |M^OA> + |B>_M |M^OB>) (|S^OA> + |S^OB>)

t₁+Δt:   (|A>_M |M_A^OA>  + |B>_M |M_B^OB>) (|S^OA> + |S^OB>)

t₂:        |A>_S |M_A^OA> |S_A^OA> + |B>_S |M_B^OB> |S_B^OB>

At t₁, the event between O and M correlates their positions, thus eliminating incompatible terms and ultimately entangling O with M so that they are no longer separable.  At t₁, there is no M that can show O in a superposition (of position eigenstates relative to M). 

Eq. 3 assumes that the event correlating the scientist to the rest of the system does not occur until time t₂.  It assumes that at t₁, |S> is separable from (i.e., unentangled/uncorrelated with) states of device M and object O and remains separable until an entangling event at time t₂.  If that’s true, then while |S> can be written as |S^OA> + |S^OB> (as above), it can also be written in lots of incompatible ways whose mathematical relevance depends on the nature of the measurement event that correlates S to M and O.  However, for |S> to be separable at t₁, there cannot have already been an event that correlates S to M and O.  Is that true?  I will argue below that because M and S are already very well correlated in position (i.e., |A>_M ≈ |A>_S and  |B>_M ≈ |B>_S), the event at t₁ correlating the positions of O and M is one in which M measures the position of O relative to S, which ultimately correlates the positions of O and S, preventing S from being able to measure O or M in a relative superposition.

Prior to the correlation event at t₁, object O can be written as |A>_M + |B>_M (i.e., the position basis relative to M), |P₁>_M + |P₂>_M + |P₃>_M + ... (i.e., the momentum basis relative to M), and various other ways depending on the measurement basis.  It is the correlation event that determines which basis and thus brings into existence one set of possibilities versus another.  So it is the correlation event between M and O, which measures O in the position basis relative to M, that brings into actual existence states |A>_M and |B>_M.  That is to say, after t₁, states |A>_M and |M^OB> are no longer compatible because O in fact was measured in the position basis by M and state |A>_M is what was measured by |M^OA> (just as state |B>_M is what was measured by |M^OB>).  Relative to M at t₁, O is no longer in superposition; it is in fact located at either A_M or B_M.  One might object with the clarification that “it is in fact located at either A_M or B_M relative to M,” but that’s redundant as positions A_M or B_M already reflect reference to device M.  The correlation event at t₁, as a matter of fact, localizes the object O at either A_M or B_M.  The only question is what meaning these positions have, if any, for scientist S. 

In other words, in an important sense, the event at t₁ does correlate the scientist to the object: she now lives in a universe in which O is located at A_M or one in which O is located at B_M, because that is exactly what it means for her to say that device M measured the position of O at t₁.  Said another way, she in fact lives in a universe in which device M has measured object O at A_M or one in which M has measured O at B_M, even though she does not yet know which, and whether or not |A>_M and |B>_M are semiclassical position eigenstates from her perspective.  This is necessarily true, for that is exactly what it means to assert that a measurement event at t₁ correlates M and O. 

This point is so important and fundamental that it is worth repeating.  The statement, “M measured the position of O,” where O was initially in state |A>_M + |B>_M, means that either O was localized at A_M or else at B_M; if it did not measure O at one of those locations, then “M measured O” has no meaning.  So when M measures O at t₁, object O is no longer in superposition |A>_M + |B>_M; scientist S now lives in a world in which device M has measured the position of object O, and that position is either A_M or B_M, not a superposition.  Proponents of U and/or MWI are certainly free to say that M measured O at both A_M and B_M in different worlds.  Perhaps the universe “fissions” so that one device, in state |M^OA>, is correlated to the object located at A_M while another, in state |M^OB>, is correlated to the object located at B_M.  In that case, scientist S also fissions so that one scientist – let’s call her state |S^OAm> – is correlated to |A>_M |M^OA> and another, in state |S^OBm>, is correlated to |B>_M |M^OB>.

Thus the object O at time t₁ is not in superposition |A>_M + |B>_M from the scientist’s (or anyone’s) perspective, but that does not tell us anything about whether the object O is in a superposition relative to scientist S or whether a position measurement by S on O would have some guaranteed (if unknown) outcome.  Specifically, consider the scientist in state |S^OAm> who is correlated to the object in state |A>_M.  If, for example, |A>_M = |A>_S + |B>_S (in other words, if the location of O at A_M is itself a superposition over locations A_S and B_S) then O remains in a superposition relative to S.  Scientist S would remain uncorrelated to the object’s position until after she measures it.  The problem with this scenario is twofold, as broached in previous sections.  First, if |A>_M is indeed uncorrelated to |A>_S, then the device’s macroscopic pointer state, as observed by the scientist at t₂, will necessarily be uncorrelated to the measurement that the scientist intended to make – specifically, the location of O at A_S or B_S.  But even if one is willing to reject the phrase “quantum measurement” as an oxymoron, the bigger problem is that there is no physical means, even in principle, by which states |A>_M and |A>_S, which were well correlated at t₀, could become adequately uncorrelated by some arbitrary time t₁.

So, given that |A>_M ≈ |A>_S and |B>_M ≈ |B>_S at t₀ through to time t₁, then just as the object O is no longer in superposition |A>_M + |B>_M at t₁, it is also not in superposition |A>_S + |B>_S.  In this case, the scientist (in state |S^OAm>) who is correlated to the object in state |A>_M is also correlated to the object in state |A>_S, which implies that the scientist is also in state |S^OA> – i.e., she now lives in a universe in which object O was localized at A_S at t₁ and she will not measure or observe anything in conflict with that fact.  Thus, if preexisting correlations between M and S are such that |A>_M ≈ |A>_S and |B>_M ≈ |B>_S, then S is not separable from M and O at t₁ because the event that correlates the positions of M and O will simultaneously correlate the positions of S and O.  Therefore, once the positions of M and O have been correlated, there is no time period – not just a small time, but zero time – in which S is separable and can measure M or O in a superposition.

An alternative explanation is this.  The correlation event at t₁ brings into existence |A>_M alongside |M^OA> (as well as |B>_M alongside |M^OB>).  But because |A>_M ≈ |A>_S and |B>_M ≈ |B>_S , both |A>_S and |B>_S are also inevitably brought into existence.  But |A>_S is a state of object O that is located at A_S relative to S; if it exists, then there must be a corresponding scientist state |S^OA> that would measure O at A_S.

Prior to the correlating event at t₁, the states of object O and device M could have been written, mathematically, in uncountably different ways depending on the chosen basis, but that freedom disappears upon the basis-determining correlation event.  The basis of measurement is what calls into existence the various possible states of O and M.  The only question is whether that correlating event can affect the existence of possible states of other objects to which M is already correlated.  I think the answer is clearly yes: if a correlating event can call into existence state |A>_M, which implies the existence of correlated state |M^OA>, and if |A>_M ≈ |A>_S, does this not also imply the existence of correlated state |S^OA>?  In light of the above analysis, Eq. 3 is corrected as follows:

Corrected Equation 3:

t₀:         (|A>_S + |B>_S) |M> |S> ≈ (|A>_M + |B>_M) |M> |S>

= (|A>_M + |B>_M) (|M^OA> + |M^OB>) (|S^OAm> + |S^OBm>)

t₁ (event correlating positions of O and M):   (|A>_M |M^OA>  + |B>_M |M^OB>) (|S^OAm> + |S^OBm>)

= |A>_M |M^OA> |S^OAm> + |B>_M |M^OB> |S^OBm>

≈ |A>_S |M^OA> |S^OA> + |B>_S |M^OB> |S^OB>

t₁+Δt:   |A>_S |M_A^OA> |S^OA> + |B>_S |M_B^OB> |S^OB>

t₂:         |A>_S |M_A^OA> |S_A^OA> + |B>_S |M_B^OB> |S_B^OB>

So what’s wrong with Eqs. 1 and 3?  It’s simple.  They fail to consider the effect of preexisting correlations between systems.  By assuming that O does not correlate with S at t₁ (allowing O and M to exist in superpositions relative to S until t₂), it follows that M cannot correlate to S, which is possible only if |A>_M ≠ |A>_S at t₁. But not only is this a physically impossible evolution if |A>_M ≈ |A>_S at t₀, it implies that the measuring device M didn’t (and therefore cannot) succeed.  Said differently: If device M measures O relative to S, then Eq. 1 is wrong at t₁ (because the correlation with S would be simultaneous and therefore S can’t show superposition), but if device M does not measure O relative to S, then Eq. 1 is wrong at t₂ because S does not get correlated to O’s location relative to him (and the device M is useless). 

The problem with Eqs. 1 and 3 is that they assume that S’s observation of M’s macroscopic pointer state at t₂ is the event that correlates S with O.  That assumption is indeed the very justification for SC, because it allows a nonzero time period (t₂ – t₁) in which a cat, whose fate is correlated to some quantum event, exists (and can in principle be measured) in a superposition state relative to an external observer.  If the observer remains uncorrelated to the outcome of the quantum event until after observing the cat is its “macroscopic pointer state” of |dead> or |alive>, then the observer can (in principle) show SC in a superposition over these two states prior to his observation.  But as we can see in the above Corrected Eq. 3, the event correlating the positions of O and S – which is the same one correlating the positions of O and M – is independent of M’s future macroscopic pointer state and whether or not S observes it.

F.         Contradictions Abound

I have argued above that the statement, “M measured the position of O at t₁,” only has meaning if it also correlates the scientist (and any other observer) to a world in which the object is measured at position A_M (or one in which the object is measured at B_M).  And because positions relative to M are so well correlated to positions relative to S (and every other large object), the statement “The positions of M and O are correlated at t₁” necessarily implies “The positions of S and O are correlated at t₁.”  There is no time period after t₁ in which O or M are (or can be demonstrated) in a superposition relative to her.  In Corrected Eq. 3, I have argued that the correlation event between M and O also correlates S to O by creating states |S^OAm> and |S^OBm> so as to produce entangled state |A>_M |M^OA> |S^OAm> + |B>_M |M^OB> |S^OBm>, and that in this state |S> appears to be inseparable. 

Despite my analysis in the previous sections, devout adherents of the assumption of U (and the in-principle possibility of creating SC, for example) are unlikely to be swayed and will insist that |S> is separable at t₁.  So let me accommodate them.  What would be required to maintain |S> as separable at t₁ to ensure that S can measure O and M in a superposition?  Easy!  Just set up the experiment so that |A>_M = |B>_M.  That would yield a combined state in which |S> is certainly separable, but it is also one in which device M didn’t actually measure anything.  So, starting from a situation in which “M measured the position of O at t₁,” in which case scientist S becomes simultaneously entangled to O by nature of that measurement, all we must do to ensure the separability of S is to change the world so that it is not the case that “M measured the position of O at t₁.”  In a very real sense, the only way to separate |S> from the entangled state caused by the correlation event between M and O is to retroactively undo that correlation event.  In other words, the statement “M measured O at t₁” implies a correlation with S that renders it inseparable, unless we are able to “undo” (or make false) the statement.

And lest I be accused of arguing tongue-in-cheek, let me point out an intriguing fact about U, nearly absent from the academic literature. Ultimately, for S to measure the correlated system M/O in a superposition relative to her, she must measure it in an appropriate basis that would reveal interference effects.  Crucially, the measurement process in that basis is one that would by necessity reverse the process that correlated M and O and would thus “undo” the correlation.  For instance, when someone asserts that SC can be created and measured in an appropriately designed interference experiment, such an experiment is necessarily one that would “turn back the clock” and undo every correlation event.[14]

Let’s forget for a moment how ridiculously technologically difficult it would be to perfectly time-reverse all the correlating events inside the SC box.  Here is a much bigger problem.  If we open the box and look – that is, measure the cat in basis {|dead>,|alive>} – we will never obtain evidence that the cat (or the system including the cat) was ever in a superposition.  But if we somehow succeed in measuring the system in a basis that would reveal interference effects, then it will retroactively undo every correlation and un-fact-ify every fact that could potentially evidence the existence of a cat in state |dead> + |alive>.  So in neither case is there, or can there be, any scientific data to assert that SC is an actual possibility (which follows from the inference of U).  SC cannot be empirically confirmed because any measurement that could demonstrate the necessary interference effects is one that retroactively destroys any evidence of SC.[15]  On this basis alone, the assertion that SC is a physically real possibility, which follows from the assumption of U, is simply not scientific.  Let me elaborate.  Consider this statement:

Statement Cat: “The measurement at time t₁ of a radioactive sample correlates to the integrity of a glass vial of poison gas, and the vial’s integrity correlates at time t₂ to the survival of the cat.” 

Let’s assume this statement is true; it is a fact; it has meaning.  A collapse theory of QM has no problem with it – at time t₁, the radioactive sample either does or does not decay, ultimately causing the cat to either live or die.  According to U, however, this evolution leads to a superposition in which cat state |dead> is correlated to one term and |alive> is correlated to another.  Such an interpretation is philosophically baffling, leading countless students and scholars wondering how it might feel to be the cat or, more appropriately, Wigner’s Friend.  Yet no matter how baffling it seems, proponents of U simply assert that a SC superposition state is possible because, while technologically difficult, it can be demonstrated with an appropriate interference experiment.  However, as I pointed out above, such an experiment will, via the choice of an appropriate measurement basis that can demonstrate interference effects, necessarily reverse the evolution of correlations in the system so that there is no fact at t₁ (to the cat, the external observer, or anyone else) about the first correlation event nor a fact at t₂ about the second correlation event.  In other words, to show that U is true (or, rather, that the QM wave state evolves linearly in systems at least as large as a cat), all that needs to be done is to make the original statement false:

1)         Statement Cat is true;[16]

2)         U is true;

3)         To show U true, Statement Cat must be shown false.

4)         Therefore, U cannot be shown true.

This is nonsense.  To summarize: U is not directly supported by empirical evidence but is rather an inference from data obtained from microscopic systems.  The inference of U conflicts with empirical observations of macroscopic systems, giving rise to the measurement problem and subjecting the inference of U to a higher standard of proof, the burden of which lies with its proponents and remains unmet.  However, the nature of the physical world seems to enforce a kind of asymptotic size limit above which interference experiments, and verification of U in the realm in which it causes the measurement problem, seem FAPP impossible.  I argued in Section II(d) that this observation serves as evidence against an inference of U, providing a further hurdle to the proponent’s currently unmet burden of proof.

I then provided several novel logical arguments in Section III showing why preexisting entanglements between a scientist and measuring device guarantee that a measurement correlating the positions of the device and an object in superposition simultaneously correlate the positions of the scientist and the object.  As a result, there is no time at which the device is or can be measured in a superposition relative to the scientist, in which case U is false because there are at least some macroscopic superpositions, such as SC and WF, that cannot be verifiably produced, even in principle.  Further, I showed that even if such an interference experiment could be done, such an experiment would, counterintuitively, not show U to be true.  That is because if U is true then it applies to a statement about a series of events (measurements, correlations, etc.), but showing that U applies to that statement requires showing that statement to be false.  This contradiction confirms that U cannot, even in principle, be verified.

The final point I’d like to bring up is this.  Undoing a correlation between two atoms that are not themselves well correlated to other objects in the universe may not be technologically difficult.  The statement, “Two atoms impacted at time t₁” only has meaning to the extent there is lasting evidence of that impact.  An experiment or process that time-reverses the impact can certainly undo the correlation, but then there is just no fact (from anyone’s perspective) about the original statement.  Quantum eraser experiments (e.g., Scully and Drühl (1982) and Kim et al. (2000)) are intriguing examples of this.

However, everything changes for macroscopic objects; cats, stars, and dust particles are already so well correlated due to past interactions that trying to decorrelate any two or more such objects is hopeless.  Perhaps the analysis of Section III can be boiled down to something like, “Preexisting correlations between M and S, which are large objects with insignificant relative coherence lengths, prevent M from ever existing or being measured in superposition relative to S.  When M correlates to O, it does not inherit the superposition of O independently of S (as suggested by linear dynamics); rather, S correlates to O simultaneously and transitively with M.”

Due to this transitivity of correlation, universal entanglement pervades the universe.  Everything is correlated with everything else and any experiment that aims to demonstrate a cat in quantum superposition by measuring it in a basis that decorrelates it from other objects is doomed to fail, not merely as a practical matter but in principle.  Even if there were a way to undo the correlations between the cat, the vial of poison, and the radioisotope, this could only be done by someone who was not already well correlated to the cat and who could manage to remain uncorrelated to it during the experiment.  This, in light of the prior analysis, is so ridiculously untenable that it warrants no further discussion.

REFERENCES

Aaronson, S., Atia, Y. and Susskind, L., 2020. On the Hardness of Detecting Macroscopic Superpositions. arXiv preprint arXiv:2009.07450.

Aharonov, Y. and Kaufherr, T., 1984. Quantum frames of reference. Physical Review D, 30(2), p.368.

Albrecht, A. and Phillips, D., 2014. Origin of probabilities and their application to the multiverse. Physical Review D, 90(12), p.123514.

Deutsch, D., 1985. Quantum theory as a universal physical theory. International Journal of Theoretical Physics, 24(1), pp.1-41.

Giacomini, F., Castro-Ruiz, E. and Brukner, Č., 2019. Quantum mechanics and the covariance of physical laws in quantum reference frames. Nature communications, 10(1), pp.1-13.

Goldstein, S., 1987. Stochastic mechanics and quantum theory. Journal of Statistical Physics, 47(5-6), pp.645-667.

Kim, Y.H., Yu, R., Kulik, S.P., Shih, Y. and Scully, M.O., 2000. Delayed “choice” quantum eraser. Physical Review Letters, 84(1), p.1.

Loveridge, L., Busch, P. and Miyadera, T., 2017. Relativity of quantum states and observables. EPL (Europhysics Letters), 117(4), p.40004.

Rovelli, C., 1996. Relational quantum mechanics. International Journal of Theoretical Physics, 35(8), pp.1637-1678.

Scully, M.O. and Drühl, K., 1982. Quantum eraser: A proposed photon correlation experiment concerning observation and" delayed choice" in quantum mechanics. Physical Review A, 25(4), p.2208.

Zych, M., Costa, F. and Ralph, T.C., 2018. Relativity of quantum superpositions. arXiv preprint arXiv:1809.04999.

---

[1] Having said that, if the particle had actually been in state |A> + |B>, then a future detection would also be consistent with its having been localized in slit A; only after many such experiments will the appearance (or lack) of an interference pattern indicate whether the original state had been |A> or |A> + |B>.

[2] We view the world as eigenstates of observables, so if Strong Relativity is correct, then so must the cat.  There is nothing special in this example about choosing the live cat’s perspective.  From the perspective of the dead cat, the lab is in the following equally ridiculous superposition: |lab that would measure a dead cat, which isn’t surprising, because it is dead> + |lab that is so distorted, whose measuring devices are so defective, whose scientists are so incompetent, that it would measure a dead cat as alive>.  The point of this example is to show that the impossibility of SC follows almost tautologically from the Strong Relativity of quantum superpositions.

[3] |A>_M ≈ |A>_S, for instance, does not say that location A is the same distance from M as from S.  Rather, it says that location A relative to M is well correlated to location A relative to S; there is zero (or inconsequential) quantum fuzziness between the locations; M and S see point A as essentially the same location.

[4] A SC state |alive> + |dead> corresponds to many macroscopic delocalizations, whether or not the centers of mass of |alive> and |dead> roughly correspond.  For instance, a particular brain cell in a cat in state |alive> would be located a significant distance from the corresponding brain cell in a cat in state |dead>.

[5] Unless otherwise stated, the word “superposition” in this analysis generally refers to a superposition of distinct semiclassical position eigenstates.

[6] The standard narrative does not really distinguish between the state at t₁ and t₁+Δt so I’ll treat them as the same time in the following equation.

[7] No collapse or reduction of the wave function is assumed in this example or anywhere else in this paper.  Fig. 1b simply shows the correlation between detection in slot (a) and location A_S; there would also be a correlation (not shown) between detection in slot (b) and location B_S.

[8] Actually, he can’t know this.  Whether or not S is “isolated” from M, the speed of light limits the rate at which S might learn about O’s localization.

[9] Although not all commentators are particularly forthright about this; Deutsch (1985) hides the complexity and difficulty of such a basis by representing them mathematically with a few symbols. 

[10] To clarify: if the object’s state is |A>_S at t₀, then physical evolution of the object over time limits where the object might be found in the future, such that scientist S in state |S^OA> will never find object O at a location that is logically inconsistent with its state |A>_S at t₀.

[11] Again, throughout this analysis I assume that U is true.  For clarity, a collapse theory of QM would assert that after the correlation event at t₁, the scientist assumes either state |S^OA> or |S^OB> – that is, after the measurement, he will observe that the state of object O has collapsed into either state |A>_S or |B>_S.  On the other hand, MWI would assert that after the event, both scientists exist in different worlds, one correlated to localization of object O at A and the other at B.  But until the correlation event, no theory or interpretation of QM claims that there are any scientists in states |S^OA> or |S^OB>.

[12] For instance, if measurement event correlates the momenta of O and M instead of position, then the term |B>_S |S^OA> will not, as a mathematical matter, disappear, but only because it can be written as a series of terms that includes, among others: |object has momentum P> |scientist will not measure object’s momentum other than P>, where P is some semiclassical momentum eigenstate.

[13] Actually, this is not a required assumption.  Whether or not device M is designed properly, M in state |M^OA> cannot evolve to any state, macroscopic or not, that is correlated to object O having been located at orthogonal position B_M.  In other words, if M in state |M^OA> evolves to a macroscopic pointer state pointing to “B,” then we can conclude that M failed as a measuring device.

[14] Aaronson et al. (2020) correctly point out that being able to confirm a cat in a superposition requires “having the ability to perform a unitary that revives a dead cat.” 

[15] This assertion is true for all observers, including the cat.  If such an interference experiment could actually be performed, then no time elapsed from the perspective of the cat (and everything inside the box).  From the cat’s perspective, it never entered a SC superposition and thus there is nothing that it’s like to experience a SC (or WF) superposition.  Even if an external observer would measure time elapsed throughout the interference experiment – which I think is doubtful for many reasons that exceed the scope of this paper – the experiment is necessarily one such that there is no fact about the happening of any correlation events inside the SC box.

[16] Of course, I can certainly show, empirically, that Statement Cat is true, simply by setting up the experiment and watching it progress.

The Measurement Problem and Bad Assumptions

I recently came to the realization that the assumed universal linearity/applicability of quantum mechanics (an assumption called “U”) cannot be empirically verified, as I discuss in this paper, this paper, this post, this post, and this update. 

This opinion is so unorthodox and so seemingly absurd (at least within the physics community) that the arXiv preprint server, which is not peer reviewed, literally rejected both of the above papers, presumably (although they won’t tell me) on the basis that it questions the “obvious” fact that macroscopic quantum superpositions of any size can be created and measured in principle. 

As more evidence that my independent crackpot musings are both correct and at the cutting edge of foundational physics, Foundations of Physics published this article at the end of October that argues that “both unitary and state-purity ontologies are not falsifiable.”  The author correctly concludes then that the so-called “black hole information paradox” and SC disappear as logical paradoxes and that the interpretations of QM that assume U (including MWI) cannot be falsified and “should not be taken too seriously.”  I’ll be blunt: I’m absolutely amazed that this article was published, and I’m also delighted. 

Finally, the tides may be turning, and whether or not I am ever acknowledged or lent credibility, I can take solace in the knowledge that I am on to something and that I likely understand things about the universe that few other scientists do.  But I think I can take this further.  I think I can show (and indeed already have shown) that there is no experiment that can be performed, even in principle, that can falsify or verify the assumption of U. 

For today’s post, I’m going to just focus on whether U was ever a valid assumption in the first place.  If it’s not – spoiler alert: it’s not – then there was never a Measurement Problem (or black hole information paradox or SC problem, etc.) in the first place. 

By the way, as I have done in this post and this post, I like to search certain phrases just to gauge whether and to what extent certain ideas exist on the internet.  To give you an idea of just how pervasive the assumption of U is, the following search phrases on Google yield, collectively, a total of 16 results:

"quantum mechanics cannot be linear"
"quantum theory cannot be linear"
"quantum mechanics cannot be unitary"
"quantum theory cannot be unitary"
"quantum mechanics cannot be universal"
"quantum theory cannot be universal"
"quantum mechanics is not linear"
"quantum mechanics is not unitary"

That’s right: this blog might be the first place in the history of the Internet to state, in these words, that quantum mechanics cannot be universal.  Incredible.

I.          INTRODUCTION

Just as logicians are bound by the laws of physics, physicists are bound by the rules of logic.  Some of the most persistent problems and paradoxes in the foundations of quantum mechanics, many of which have been unsuccessfully tackled by physicists and mathematicians for nearly a century, persist exactly because they aren’t really physics or mathematics problems at all, but rather problems of logic. 

Consider the problems of Schrödinger’s Cat (“SC”) and its conscious cousin, Wigner’s Friend (“WF”).  If SC is characterized (neglecting normalization constants) as, “A cat in state |dead> + |alive> is simultaneously dead and alive,”[1] then SC is inherently impossible because “dead” and “alive” are mutually exclusive.  Therefore, if SC is physically possible, at least in principle, then it is patently false that a cat in state |dead> + |alive> is simultaneously dead and alive.  Indeed, the characterization of any object in a quantum superposition of eigenstates of some observable as being “simultaneously in those eigenstates” is equally problematic.

While SC is not inherently paradoxical, it is more than a little odd.  The generally accepted conclusion that a SC state is possible in principle follows directly from the assumption that the mathematics of quantum mechanics (i.e., its linear or unitary evolution) applies universally at all scales, including both electron and cat.  This assumption leads to the century-old measurement problem (“MP”) of quantum mechanics (“QM”).  The measurement problem is actually a paradox, meaning that it comprises logically incompatible assumptions.  Contradictions are necessarily false and therefore cannot exist in nature.  If the conjunction of statements A and B, for example, leads to a contradiction, then at least one of statements A and B is false.  Often, MP has been characterized as the conjunction of three or more assumptions (e.g., Maudlin (1995) and Brukner (2017)); the logical incompatibility of these assumptions has been shown many times (e.g., Frauchiger and Renner (2018) and Brukner (2018)).  A simpler characterization of MP, reducing it to two assumptions, has been provided by Gao (2019):

P1) The mental state of an observer supervenes on her wave function;

P2) The wave function always evolves in accord with a linear dynamical equation (such as the Schrödinger equation).

Assumption P2 is often characterized as the “universality” of QM, in that the rules of QM are assumed to apply universally at all scales.  Kastner (2020) correctly notes that “unitary-only evolution” is a better description than “universality” because, she argues, a complete theory of QM (if there is one) will necessarily apply universally but its wave equations may not evolve in a purely unitary or linear fashion.  Whether meaning “universal” or “unitary-only,” in this paper I’ll generally refer to assumption P2 as “U.”

Contradictions do not exist in nature.  Because at least one of P1 and P2 is indeed false, a simultaneous belief in both is due to faulty reasoning.  The measurement problem is not a problem with nature; it is a problem with us.  It is either the case that P1 is the result of improper assumptions and/or reasoning, that P2 is the result of improper assumptions and/or reasoning, or both.  My goal in this paper is to attack P2 on a variety of grounds. 

II.        EVALUATING UNIVERSALITY

A.        What’s the Problem?

The measurement problem is inextricably related to SC, WF, etc., and might be colloquially phrased as, “If a cat can exist as a superposition over macroscopically distinct eigenstates |dead> and |alive>, then why do we always see either a dead or a live cat?”  Or: “If quantum mechanics applies universally at all scales (or wave functions always evolve linearly), then why do we never observe quantum superpositions?”  Or even better: “Why don’t we see quantum superpositions?” 

As Penrose (1999) points out, MP is actually a paradox and any solution to it requires showing that at least one of its assumptions is incorrect.  All formulations of MP depend on the assumption of U.  Of course, MP would be solved if it were shown that QM wave states did not always evolve linearly, such as above certain scales.  After 100 years, why has this not yet been shown?  Perhaps this is the wrong question.  The first questions we should ask are: were we justified in assuming U in the first place?  Has it been empirically demonstrated?  Can it be empirically demonstrated?

U is itself an inference.  The question is not whether logical inferences can be made in science –they can and must.  One can never prove that a scientific hypothesis or law always holds; rather, it can only be adequately verified to permit such an inference, subject always to the possibility of experimental falsification.  However, U is a very special kind of inference, one that I will argue in the following sections is invalid.  First, U has been verified only in microscopic regimes.  No experiment has shown it to apply to macroscopic regimes; there is no direct experimental evidence for the applicability of the linear dynamics of QM to macroscopic systems.  Second, the lack of such evidence is not for lack of trying.  Rather, there seems to be a kind of asymptotic limit to the size of a system to which we are able to gather such evidence.  Third, U gives rise to the measurement problem – that is, it conflicts with what seems to be good empirical evidence that linear QM dynamics do not apply in most[2] cases.  These together, as I will argue, render U an invalid inference.   Further, even if one disagrees with this argument, the burden of proof rests not with the skeptics but with those who endorse an inference of U.  

Regarding the first point – that U has been verified only in the microscopic realm – there are certainly those who choose to tamper with the colloquial meanings of the words “microscopic” and “macroscopic,” or attempt to redefine “mesoscopic” as “nearly macroscopic,” to bolster their case.  Some may include as “macroscopic quantum superpositions” atoms in superposition over position eigenstates separated by a meter, or “macroscopic” (though barely visible) objects in superposition over microscopically-separated position eigenstates (e.g., O’Connell et al. (2010)).  I regard this as sophistry, particularly when such examples are used as empirical evidence that the creation and measurement of truly macroscopic superpositions, such as SC, are mere technological hurdles.  Nevertheless, I will assume that any physicist acting in good faith will readily admit that there is currently no direct empirical evidence that linear QM evolution applies to a cat, a human (e.g., WF), or even a virus.  That lack of experimental evidence renders an inference that QM applies universally especially bold.  And bold inferences are not necessarily problematic – until they come into conflict with other observations.

Consider these statements:

A1) Newton’s law of gravity applies universally.

A2) The observed perihelion of Mercury is in conflict with Newton’s law of gravity.

Statement A1 was a valid inference for a very long time.  The conjunction of these statements, however, is a contradiction, implying that at least one of them is false.  A contradiction sheds new doubt on each statement and increases the evidence necessary to verify each unless and until one of the assumptions is shown false.  Despite enormous quantities of data supporting an inference of A1, conflicting evidence ultimately led Einstein to reject A1 and formulate general relativity.

The measurement problem is such a paradox; it is the conjunction of two or more statements that lead to a contradiction.  If there were no paradox, we might reasonably have inferred U based only on the limited experimental data showing interference effects from electrons, molecules, etc.  However, U is in direct logical conflict with other statement(s) the veracity of which we seem to have a great deal of evidence.  Therefore, to justify the inference of U, we need more than a reason: we need a good reason.  However, given that the paradox arose essentially simultaneously with quantum theory, leading Erwin Schrödinger to propose his hypothetical cat as an intuitive argument against U, the burden of proof has always lain with those who assert U.  Have they met their burden?  Do we have good evidence to support the inference of U?

B.        Fighting Fire with Fire

Many (perhaps most) physicists have never questioned the assumption of U, and once asked whether we have good evidence to support the inference of U may regard the question itself as nonsense.  “Of course the wave function always evolves linearly – just look at the equations!”  Indeed, standard QM provides no mathematical formalism to explain, predict, or account for breaks in linearity.  Some collapse theories (such as the “GRW” spontaneous collapse of Ghirardi, Rimini, and Weber (1986) and gravitational collapse of Penrose (1996)) do posit such breaches, but no experiment has yet confirmed any of them or distinguished them from other interpretations of QM.  It is thus tempting, when evaluating U, to glance at the equations of QM and note that they do, indeed, evolve linearly.  But the question isn’t whether the equations evolve linearly, but whether the physical world always obeys those equations, and the answer to that question does not appear within the QM formalism itself.[3]

Modern physicists, who rely heavily on mathematics to proceed, typically demand rigorous mathematical treatment in addressing and solving physics problems.  Ordinarily, such demands are appropriate.  However, MP arises directly as a result of the mathematics of QM, in which the Schrödinger equation evolves linearly and universally.  Because MP is itself a product of the mathematics of QM, its solution is inherently inaccessible via the symbolic representations and manipulations that produced it.  If the math itself is internally consistent – and I have no reason to believe otherwise – then you cannot use the math of QM as evidence that the math of QM is always correct.[4]  You can, however, use empirical evidence to support such an inference.  Do we have such evidence?

C.        Empirical Data

The rules of QM allow us to make probabilistic predictions on the outcomes of measurements that differ from the expectations of classical probability.  In a very real sense, this is both how QM was discovered[5] as well as what makes an event quantum mechanical.  Wave functions of objects contain a superposition of terms having complex probability amplitudes, and interference between those terms in an experiment can alter outcome probabilities.  A demonstration of quantum effects, then, depends on an interference experiment – i.e., an experiment that demonstrates interference effects in the form of altered probability distributions.  In a very real sense, quantum mechanics is fundamentally about making probabilistic predictions that depend on whether interference effects from terms in a coherent superposition are relevant.[6]

It is often claimed that no violation of the linearity of QM has ever been observed, or that no experiment has ever shown the non-universality of QM.  In fact, this is the only empirical scientific evidence that physicists can cite to support the inference of U.  How good is this evidence?  Consider the following claim, perhaps supported by the vast majority of physics:

“The mathematics of QM applies to every object subjected to a double-slit interference experiment, no matter how massive, because no experiment has ever demonstrated a violation.” 

Indeed, double-slit interference experiments (“DSIE”) have been successfully performed on larger and larger (though still microscopic) objects, such as a C₆₀ molecule.  (Arndt et al. (1999).)  However, to evaluate the extent to which this evidence supports an inference of U, it is necessary to consider how DSIEs are set up and performed. 

Nature – thanks to the Heisenberg Uncertainty Principle – creates superpositions ubiquitously. Quantum uncertainty, loosely defined for a massive object as , guarantees dispersion of quantum wave packets, thus increasing the size of location superpositions over time. However, interactions with fields, photons, and other particles ever-present in the universe constantly “measure” the locations of objects and thus decohere[7] these superpositions.  (See, e.g., Tegmark (1993) and Joos et al. (2013).) This decoherence, which I’ll discuss in greater detail in the next section, explains both why we don't observe superpositions in our normal macroscopic world and also why visible interference patterns from quantum superpositions of non-photon objects[8] are so difficult to create.

For instance, let's consider the non-trivial process, first performed by Davisson and Germer in 1927, of producing an electron in (non-normalized) superposition state |A> + |B>, where |A> is the wave state corresponding to the electron traversing slit A while |B> is the wave state corresponding to the electron traversing adjacent slit B in a double-slit plate. Electrons, one at a time, are passed through (and localized by) an initial collimating slit; quantum uncertainty results in dispersion of each electron’s wave state at a rate inversely proportional to the width of the collimating slit. If the process is designed so that adequate time elapses before the electron’s wave state reaches the double-slit plate, and without an intervening decoherence event with another object, the electron’s wave will be approximately spatially coherent over a width wider than that spanned by both slits. If the electron then traverses the double-slit plate, its wave function becomes the superposition |A> + |B>.  Because such a superposition does not correspond to its traversing slit A or traversing slit B, it carries no “which-path” information about which slit the electron traversed.  If each electron is then detected at a sensor located sufficiently downstream from the double-slit plate, again without an intervening decoherence event with another object, the spatial probability distribution of that electron’s detection will be calculable consistent with quantum mechanical interference effects. This lack of which-path information (thanks to successfully preventing any decohering correlations with other objects in the universe) implies that the electron’s superposition coherence was maintained, and thus the rules of quantum mechanics (and not classical probability) would apply to probability distribution calculations.[9]

Because the dispersion of an object’s wave function is directly proportional to Planck’s constant and inversely proportional to its mass, the ability to demonstrate the wave-like behavior of electrons is in large part thanks to the electron’s extremely small mass.[10] The same method of producing superpositions – waiting for quantum dispersion to work its magic – has been used to produce double-slit interference effects of objects as large as a few hundred and perhaps a couple thousand atoms.  (See, e.g., Eibenberger et al. (2013) and Fein et al. (2019).)  However, the more massive the object, the slower the spread of its wave state and the more time is available for an event to decohere any possible superposition.  Are there other methods, besides quantum dispersion, to prepare an object for a DSIE?  I don’t know.  However, every successful DSIE to date has indeed depended on quantum dispersion of the object’s wave packet, and it is this evidence, not the hypothetical possibility of other experiments, that is available to support (or not) an inference of U.

So, within the data available to support the inference of U, performing a DSIE by passing an object through slits A and B separated by some distance d first requires making the object spatially coherent over a distance exceeding d.  To get the object in the superposition |A> + |B> to subsequently show interference effects, you have to provide the object in a state that is adequately quantum mechanically “fuzzy” over a distance exceeding d – that is, a state that would already demonstrate interference effects.  In other words, to do a DSIE on an object to show that it does not violate the linearity of QM, you have to first provide an object prepared so that an interference experiment would not violate the linearity of QM.

Said another way, the observation of an interference effect in a double-slit interference experiment presupposes the spatial coherence of an object over some macroscopically resolvable distance.  But the ability to produce that object (or an object of any size, at least in principle) in spatial coherence is the very assumption of U.  Measuring interference effects by an object that has already been prepared to show interference effects is not a confirmation of, or evidence for, the universal linearity of QM.  What it does show is that QM is linear at least to that level.  For example, if QM is indeed nonlinear through a physical collapse mechanism like that proposed by GRW, then such a collapse might be confirmed by first preparing a system in an appropriate superposition (which should, if properly measured, demonstrate interference effects), and then failing to observe interference effects.  The ability to demonstrate, for example, a C₆₀ molecule exhibiting interference effects puts a lower limit on the scale (mass, time period, etc.) to which a physical collapse mechanism would act.

My goal in this section is not to call into question the usefulness of interference experiments in demonstrating the applicability of linear QM to objects in those experiments.  My goal is to point out the logical circularity of asserting that “QM applies universally because no interference experiment has shown a violation in linearity,” given that interference experiments are only performed on objects that have already been successfully prepared in a state that can demonstrate interference.  The experimental difficulty is not in showing interference effects from an object prepared to show interference effects; the difficulty is in preparing the object to show interference effects.  So what do the empirical data tell us about the difficulty in preparing objects to show interference effects?  And do those data support an inference of U?

D.        Empirical Data Revisited

It may well be true that 100% of interference experiments have failed to show nonlinearity, but if all experiments performed so far only probe the microscopic realm and – more importantly – if these experiments are quite literally chosen because they only probe the microscopic realm, then the fact that no interference experiment has ever shown a violation of linearity is simply not evidence to support the inference that QM is universally linear.

If the reason that interference experiments are chosen to probe only the microscopic realm is merely that of convenience, or insufficient grant funding, or technological limitation, then my argument would be limited only to the conclusion that current empirical data do not support an inference to U, in which case the proponent of U has failed to meet any reasonable burden of proof.  However, if it turns out that interference experiments are chosen to probe only the microscopic realm because there is something about the physical world, directly related to the size of systems, that makes it impossible at least for all practical purposes (“FAPP”) to probe larger systems, then this would serve as empirical evidence against U, in which case the proponent’s unmet burden of proving the inference of U is far, far greater.

Here are a few empirical facts: a) so far, the largest object to show interference effects in a DSIE is a molecule consisting of around two thousand atoms (Fein et al. (2019)); b) these experiments have depended on quantum dispersion of an object’s wave packet to produce adequate spatial coherence; and c) the rate of quantum dispersion quickly approaches zero as the object increases in size.  I would argue that these facts, particularly our inability to prepare macroscopic object to show interference effects, constitute very good evidence against U.[11]

Let me elaborate.  If an experimenter can rely on quantum dispersion to put a molecule in adequate spatial coherence to measure interference effects, why can’t he do that for a dust particle or a cat?  Consider the difficulty in performing a DSIE on a dust particle. Let's assume it is a 50μm-diameter sphere with a density of 1000 kg/m³ and it has just been localized by an impact with a green photon (λ ≈ 500nm). How long will it take for its location “fuzziness” to exceed its own diameter (which would be the absolute minimum spatial coherence allowing for passage through a double-slit plate)?  Letting  ≈ 10^-18 m/s, it would take 5x10¹³ seconds (about 1.5 million years) for the location uncertainty to reach a spread of 50μm.[12]  In other words, if we sent a dust particle into deep space, its location relative to other objects in the universe is so well defined due to its correlations to those objects that it would take over a million years for the universe to “forget” where the dust particle is to a resolution allowing for the execution of a DSIE.[13]  In this case, information in the universe would still exist to localize the dust particle to a resolution of around 50μm, but not less. Unfortunately, this rough calculation depends on a huge assumption: that new correlation information isn’t created in that very long window of time. In reality, the universe is full of particles and photons that constantly bathe (and thus localize) objects.

Thus there is a trade-off in the delocalization caused by natural quantum dispersion and localizing “measurements” caused by interactions with the plethora of stuff whizzing through space. This trade-off is heavily dependent on the size of the object; a tiny object (like an electron) disperses quickly due to its low mass and experiences a low interaction rate with other objects, allowing an electron to more easily demonstrate interference effects. On the other hand, a larger object disperses more slowly while suffering a much higher interaction rate with other objects. These observations can be quantified in terms of coherence lengths: for a particular decoherence source acting on a particular object, what is the largest fuzziness we might expect in the object's center of mass? And, if we're hoping to do a DSIE, does this fuzziness exceed the object's diameter?

Tegmark (1993) calculates coherence lengths (roughly “the largest distance from the diagonal where the spatial density matrix has non-negligible components”) for a 10μm dust particle and a bowling ball caused by various decoherence sources, as shown in Table I.  Even in deep space, cosmic microwave background (“CMB”) radiation alone will localize the dust particle to a dimension many orders of magnitude smaller than its diameter, thus ruling out any possibility for that object to become adequately delocalized (and thus adequately spatially coherent) relative to the universe to perform an interference experiment.  The prospects are far worse for a bowling ball-sized cat.

Table I.  Some values of coherence lengths for a 10μm dust particle and a bowling ball caused by various decoherence sources, given by Tegmark (1993). 

In other words, as at least a practical matter, the physical world is such that there is a size limit to the extent that quantum dispersion can be relied upon to perform a DSIE.  Having said that, no one seriously argues (as far as I know) that SC or WF could be produced, even in principle, through natural quantum dispersion.  Rather, the typical argument is that SC/WF could be produced through amplification of a quantum event via a von Neumann measurement chain.  Crucially, however, the purported ability to amplify a quantum superposition assumes universal linearity of QM, which means that it cannot be logically relied upon to contradict the argument that QM is not universally linear.  Further, there is no empirical evidence that quantum amplification ever has produced a measurable macroscopic quantum superposition.[14]  In other words, without assuming that quantum amplification can accomplish what quantum dispersion cannot – i.e., ignoring the logical circularity of assuming the very conclusion that I am arguing against – one must conclude that existing empirical evidence does not support the inference that a DSIE can in principle be performed on macroscopic objects like a cat.

As a purely empirical matter, all DSIEs that have been performed depend on quantum dispersion, which depends inversely on the size of an object, to produce the object in spatial coherence that exceeds some macroscopically resolvable distance.  Consequently, all such experiments have been chosen specifically to probe the microscopic realm, where quantum dispersion “works.”  This observation is sufficient to invalidate the inference that QM wave states evolve linearly beyond the microscopic realm, because all such experiments are chosen specifically on the basis of probing the microscopic realm. 

Having said that, this section shows that such choices for experimentation are not merely on the basis of convenience – rather, the physical world is such that interference experiments inherently become increasingly difficult at an increasing rate as the size of an object increases.  There seems to be an asymptotic limit[15] on the size of an object on which we can perform a DSIE.  Our difficulty in preparing larger objects to show interference effects is (or should be) telling us something fundamental about whether QM wave states always evolve linearly. 

Importantly, I am not asserting that the above analysis shows that performing a DSIE on a cat is impossible in principle.  Rather, it shows that a fundamental feature of our physical world is that our efforts to demonstrate interference effects for larger systems have quickly diminishing returns; the harder we try to increase the size of an object to which QM is verifiably linear, the more slowly that size increases.  There is at least some physical size (perhaps within an order of magnitude of the dust particle in Table I) above which no conceivable experiment, no matter how technologically advanced, could demonstrate interference effects.  The fact that such a size exists to physically distinguish the “macroscopic” from the “microscopic,” which, as a practical matter, forces us to choose interference experiments that probe only the microscopic regime, is strong empirical evidence against an inference of U.  In other words, the existence of a FAPP limitation, even if there is no in-principle limitation, is itself evidence against an inference of U.

E.        Burden of Proof

It is worth emphasizing that the measurement problem does not arise from the evidence that QM is linear in microscopic systems; it arises only from an inference that QM remains linear in macroscopic systems.  I have shown in the above sections that the inference of U:

·         Is not supported by any direct empirical evidence;

·         Is such that no practical or currently technologically conceivable experiment can provide direct empirical evidence; and

·         Is logically incompatible with one or more assertions (such as statement P1) for which we ostensibly have a great deal of evidence, thus giving rise to the measurement problem.

I cannot offer or conceive of any rational scientific basis on which to accept such an inference. For these reasons alone, from a scientific standpoint, MP should be dismissed – not because it has been solved, but because it should never have arisen in the first place.  MP depends on the truth of at least two statements, one of which is U.  It should be enough to show that the best empirical evidence regarding that statement is inadequate to support, and in fact opposes, the inference of U.  Not only have proponents of U failed to meet their burden of proving that an inference of U is valid, that burden, in light of the arguments in this section, is exceptional.

REFERENCES

Arndt, M., Nairz, O., Vos-Andreae, J., Keller, C., Van der Zouw, G. and Zeilinger, A., 1999. Wave–particle duality of C 60 molecules. nature, 401(6754), pp.680-682.

Brukner, Č., 2017. On the quantum measurement problem. In Quantum [Un] Speakables II (pp. 95-117). Springer, Cham.

Brukner, Č., 2018. A no-go theorem for observer-independent facts. Entropy, 20(5), p.350.

D’Ariano, G.M., 2020. No purification ontology, no quantum paradoxes. Foundations of Physics, pp.1-13.

Davisson, C. and Germer, L.H., 1927. The scattering of electrons by a single crystal of nickel. Nature, 119(2998), pp.558-560.

Eibenberger, S., Gerlich, S., Arndt, M., Mayor, M. and Tüxen, J., 2013. Matter–wave interference of particles selected from a molecular library with masses exceeding 10000 amu. Physical Chemistry Chemical Physics, 15(35), pp.14696-14700.

Fein, Y.Y., Geyer, P., Zwick, P., Kiałka, F., Pedalino, S., Mayor, M., Gerlich, S. and Arndt, M., 2019. Quantum superposition of molecules beyond 25 kDa. Nature Physics, 15(12), pp.1242-1245.

Frauchiger, D. and Renner, R., 2018. Quantum theory cannot consistently describe the use of itself. Nature communications, 9(1), pp.1-10.

Gao, S., 2019. The measurement problem revisited. Synthese, 196(1), pp.299-311.

Ghirardi, G.C., Rimini, A. and Weber, T., 1986. Unified dynamics for microscopic and macroscopic systems. Physical review D, 34(2), p.470.

Hossenfelder, S., 2018. Lost in math: How beauty leads physics astray. Basic Books.

Joos, E., Zeh, H.D., Kiefer, C., Giulini, D.J., Kupsch, J. and Stamatescu, I.O., 2013. Decoherence and the appearance of a classical world in quantum theory. Springer Science & Business Media.

Kastner, R.E., 2020. Unitary-Only Quantum Theory Cannot Consistently Describe the Use of Itself: On the Frauchiger–Renner Paradox. Foundations of Physics, pp.1-16.

Knight, A., 2020.  No paradox in wave-particle duality.  Foundations of Physics, 50(11), pp. 1723-27.

Maudlin, T., 1995. Three measurement problems. topoi, 14(1), pp.7-15.

O’Connell, A.D., Hofheinz, M., Ansmann, M., Bialczak, R.C., Lenander, M., Lucero, E., Neeley, M., Sank, D., Wang, H., Weides, M. and Wenner, J., 2010. Quantum ground state and single-phonon control of a mechanical resonator. Nature, 464(7289), pp.697-703.

Penrose, R., 1996. On gravity's role in quantum state reduction. General relativity and gravitation, 28(5), pp.581-600.

Penrose, R., 1999. The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press.

Tegmark, M., 1993. Apparent wave function collapse caused by scattering. Foundations of Physics Letters, 6(6), pp.571-590.

---

[1] Such as in this article

[2] Although, to show U false, just one counterexample is necessary.

[3] Unless you count the “projection postulate,” which some would argue is prima facie evidence that the QM equations do not always evolve linearly.

[4] Some go further and assert that the beauty and/or simplicity of linear dynamical equations are evidence for their universal applicability.  I, like Hossenfelder (2018), disagree.  Aesthetic arguments are not empirical evidence for a scientific hypothesis, despite assertions by some string theorists to the contrary.

[5] The characterization of light as discrete particle-like objects, thanks to Planck’s use of  to avoid the Ultraviolet Catastrophe and Einstein’s explanation of the photoelectric effect, showed that classical probability is inapplicable to predicting the detection outcome of individual particles in a double-slit interference experiment.

[6] Like all probability rules, a statistically significant ensemble is necessary to obtain useful information. A measurement on any object will always yield a result that is consistent with that object's not having been in a superposition; only by measuring many identically prepared objects may the presence of a superposition appear in the form of an interference pattern.

[7] The theory underlying decoherence is not incompatible with the assumption of U; in fact, many (if not most) of the proponents of decoherence specifically endorse U.  Rather, decoherence is often used to explain why it is so difficult to macroscopic objects in (coherent) superpositions.

[8] Interference effects of photons are actually quite easy to observe in part because photons do not self-interact and thus are not decohered by other radiation. Prior to the invention of lasers, a dense source of coherent photons, which confirmed light's wave-like behavior, came directly from the sun.

[9] Indeed, the existence of which-path information – that is, the existence of a correlating fact about the passage of the electron through one slit or the other – is incompatible with existence of a superposition at the double-slit plane.  (See, e.g., Knight (2020).)

[10] We might alternatively say that the de Broglie wavelength of an electron can be made sufficiently large in a laboratory so as to reveal its wave nature.

[11] Penrose (1999) suggests that the fact that we always observe measurement results is excellent empirical evidence that the QM wave function cannot always evolve linearly.

[12] Tegmark (1993) notes that macroscopic systems tend to be in “nearly minimum uncertainty states.”

[13] This estimate completely neglects the additional time necessary to subsequently measure an interference pattern.

[14] A related objection is whether it is possible to adequately isolate or shield a macroscopic object from decoherence sources long enough for dispersion to work its magic.  The answer is no, for reasons, including logical circularity, that exceed the scope of this paper.  But, like the hypothetical proposed “fix” of amplification, there is no actual evidence that shielding or isolation ever has produced a measurable macroscopic superposition.

[15] I don’t mean this in a rigorous mathematical sense.  Rather there is some rough object size below which we are able, as a practical matter, to show interference effects of the object and above which we simply cannot.  We might loosely call this size the “Heisenberg cut.”